题目内容
椭圆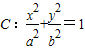 (a>b>0),直线y=k(x-1)经过椭圆C的一个焦点与其相交于点M,N,且点
(a>b>0),直线y=k(x-1)经过椭圆C的一个焦点与其相交于点M,N,且点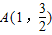 在椭圆C上.
在椭圆C上.(I)求椭圆C的方程;
(II)若线段MN的垂直平分线与x轴相交于点P,问:在x轴上是否存在一个定点Q,使得
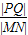 为定值?若存在,求出点Q的坐标和
为定值?若存在,求出点Q的坐标和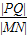 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】分析:(I)确定椭圆的焦点,利用点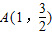 在椭圆C上,建立方程,求出几何量,即可得到椭圆的方程;
在椭圆C上,建立方程,求出几何量,即可得到椭圆的方程;
(II)直线y=k(x-1)与椭圆方程联立,利用韦达定理,确定MN垂直平分线方程,|MN|,可得P的坐标,从而可得结论.
解答:解:(I)由题意,椭圆的一个焦点为(1,0),
又∵点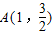 在椭圆C上,
在椭圆C上,
∴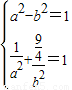
∴a2=4,b2=3
∴椭圆C的方程为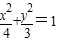 ;
;
(II)存在,
直线y=k(x-1)与椭圆方程联立可得(3+4k2)x2-8k2x+4k2-12=0,
设M(x1,y1),N(x2,y2),则 ,
,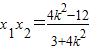 ,
,
∴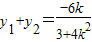
∴MN垂直平分线方程为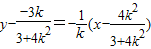
令y=0,可得x=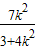
∴P(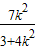 ,0),
,0),
设Q(a,0),则|PQ|=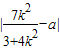
∵|MN|=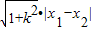 =
=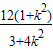 ,
,
∴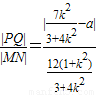 =
=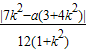
∴a=7时, =
=
∴Q(7,0).
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.
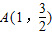 在椭圆C上,建立方程,求出几何量,即可得到椭圆的方程;
在椭圆C上,建立方程,求出几何量,即可得到椭圆的方程;(II)直线y=k(x-1)与椭圆方程联立,利用韦达定理,确定MN垂直平分线方程,|MN|,可得P的坐标,从而可得结论.
解答:解:(I)由题意,椭圆的一个焦点为(1,0),
又∵点
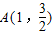 在椭圆C上,
在椭圆C上,∴
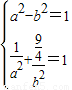
∴a2=4,b2=3
∴椭圆C的方程为
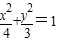 ;
;(II)存在,
直线y=k(x-1)与椭圆方程联立可得(3+4k2)x2-8k2x+4k2-12=0,
设M(x1,y1),N(x2,y2),则
 ,
,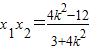 ,
,∴
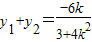
∴MN垂直平分线方程为
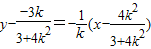
令y=0,可得x=
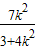
∴P(
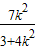 ,0),
,0),设Q(a,0),则|PQ|=
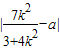
∵|MN|=
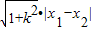 =
=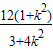 ,
,∴
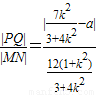 =
=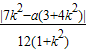
∴a=7时,
 =
=
∴Q(7,0).
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
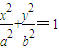 (a>b>0)的左右焦点,A为上顶点,椭圆上的点N满足:
(a>b>0)的左右焦点,A为上顶点,椭圆上的点N满足: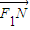 =
=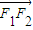 +λ
+λ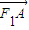 (λ∈R).
(λ∈R). ,过点N作椭圆的切线分别交左、右准线于P、Q,直线NF1、NF2分别交椭圆于C、D两点.是否存在实数m,使
,过点N作椭圆的切线分别交左、右准线于P、Q,直线NF1、NF2分别交椭圆于C、D两点.是否存在实数m,使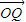 =m(
=m(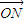 +
+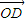 )?若存在,求出实数m的值,否则说明理由;
)?若存在,求出实数m的值,否则说明理由;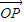 =n(
=n(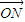 +
+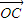 )?若存在写出n的值.
)?若存在写出n的值. (a>b>0)与双曲线
(a>b>0)与双曲线 (m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )
(m>0,n>0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )  B.
B. 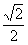 C.
C.  D.
D.