题目内容
设F1、F2是椭圆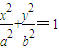 (a>b>0)的左右焦点,A为上顶点,椭圆上的点N满足:
(a>b>0)的左右焦点,A为上顶点,椭圆上的点N满足: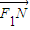 =
=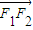 +λ
+λ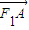 (λ∈R).
(λ∈R).(1)求实数λ的取值范围;
(2)设λ=
 ,过点N作椭圆的切线分别交左、右准线于P、Q,直线NF1、NF2分别交椭圆于C、D两点.是否存在实数m,使
,过点N作椭圆的切线分别交左、右准线于P、Q,直线NF1、NF2分别交椭圆于C、D两点.是否存在实数m,使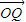 =m(
=m(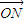 +
+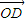 )?若存在,求出实数m的值,否则说明理由;
)?若存在,求出实数m的值,否则说明理由;(3)在(2)的基础上猜想:是否存在实数n,使
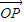 =n(
=n(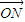 +
+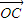 )?若存在写出n的值.
)?若存在写出n的值.
【答案】分析:(1)设N(x,y),由点N满足: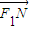 =
=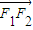 +λ
+λ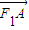 (λ∈R),将相关点的坐标代入,由向量相等的充要条件,可将N点坐标用λ表示,代入椭圆方程,得λ与a、b、c的等式,利用离心率的范围即可求得λ的范围
(λ∈R),将相关点的坐标代入,由向量相等的充要条件,可将N点坐标用λ表示,代入椭圆方程,得λ与a、b、c的等式,利用离心率的范围即可求得λ的范围
(2)由(1)知N(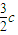 ,
,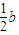 ),再由直线NF2与椭圆联立求得D(0,-b),而点Q的横坐标也已知为
),再由直线NF2与椭圆联立求得D(0,-b),而点Q的横坐标也已知为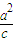 ,将这些点的坐标代入已知
,将这些点的坐标代入已知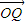 =m(
=m(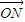 +
+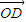 ),即可得m=
),即可得m=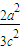 =
=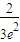 ,Q(
,Q(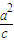 ,-
,-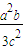 ),从而求得切线NQ的斜率,等于利用导数的几何意义求得的椭圆在点N处的切线斜率,求得椭圆离心率,进而求出m的值
),从而求得切线NQ的斜率,等于利用导数的几何意义求得的椭圆在点N处的切线斜率,求得椭圆离心率,进而求出m的值
(3)根据(2)的思路,只需求出直线NF1与椭圆的交点C的横坐标,代入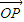 =n(
=n(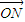 +
+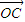 ),得m与离心率的关系,代入求得的离心率即可猜想n值
),得m与离心率的关系,代入求得的离心率即可猜想n值
解答:解:(1)设N(x,y)
∵F1(-c,0)F2(c,0),A(0,b),
∴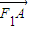 =(c,b),
=(c,b),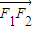 =((2c,0),
=((2c,0),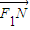 =(x+c,y)
=(x+c,y)
∵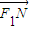 =
=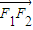 +λ
+λ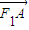 (λ∈R),
(λ∈R),
∴(x+c,y)=(2c,0)+λ(c,b),
∴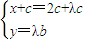
∴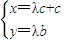 ,
,
∵N点在椭圆上,代入椭圆方程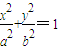
得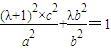
∴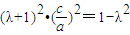 ,显然λ=-1满足等式
,显然λ=-1满足等式
若λ≠-1,则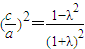
∵椭圆的离心率e=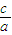 ∈(0,1)
∈(0,1)
∴0<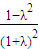 <1
<1
解得0<λ<1
∴实数λ的取值范围为(0,1)∪{-1}
(2)∵λ=
∴N(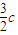 ,
,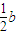 )
)
∵直线NF2的方程为y=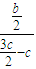 (x-c)
(x-c)
即y=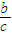 (x-c),∵此直线过点(0,-b)
(x-c),∵此直线过点(0,-b)
∴D(0,-b)
假设存在实数m,使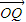 =m(
=m(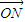 +
+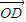 )
)
∵Q在右准线x=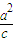 上,∴Q的横坐标为
上,∴Q的横坐标为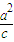 ,设纵坐标为yQ
,设纵坐标为yQ
则(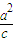 ,yQ)=m[(
,yQ)=m[(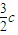 ,
,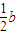 )+(0,-b)]
)+(0,-b)]
∴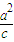 =
=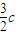 ×m,∴m=
×m,∴m=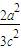 =
=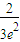 *
*
∴yQ=-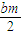 =-
=-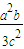
Q(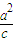 ,-
,-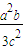 )
)
∵直线NQ的斜率为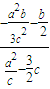 =
=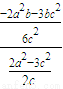 =
=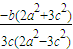 ①
①
由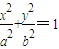 ,得椭圆在第一象限的图象的函数解析式为y=
,得椭圆在第一象限的图象的函数解析式为y=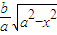
y′=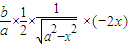 =
=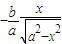
∴y′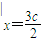 =
=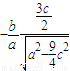 =
=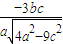
即椭圆切线NQ的斜率为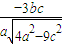 ②
②
由①②得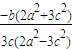 =
=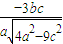
化简得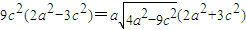
两边同除以a4,得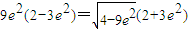
解得e2=
代入*式,得m=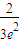 =2
=2
故存在实数m=2,使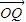 =m(
=m(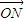 +
+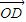 )
)
(3)∵N(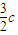 ,
,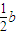 )
)
∵直线NF1的方程为y=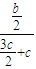 (x+c)
(x+c)
即y=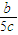 (x+c),代入椭圆方程得(1+
(x+c),代入椭圆方程得(1+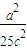 )x2+
)x2+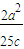 x-
x-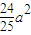 =0
=0
∴xC×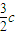 =
=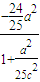
∴xC=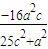 ,
,
假设存在实数n,使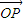 =n(
=n(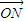 +
+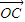 )
)
∵P在左准线x=-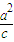 上,∴Q的横坐标为-
上,∴Q的横坐标为-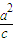 ,设纵坐标为yP
,设纵坐标为yP
则(-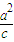 ,yP)=m[(
,yP)=m[(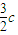 ,
,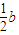 )+(
)+(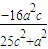 ,yC)]
,yC)]
∴-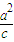 =(
=(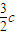 +
+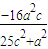 )×m,
)×m,
∴m= =
=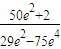
由(2)知e2=
代入上式得:m=14
故猜想存在n=14,使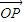 =n(
=n(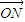 +
+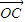 )
)
点评:本题考查了椭圆的标准方程及其几何性质,直线与椭圆的位置关系,向量与解析几何的综合运用
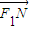 =
=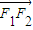 +λ
+λ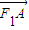 (λ∈R),将相关点的坐标代入,由向量相等的充要条件,可将N点坐标用λ表示,代入椭圆方程,得λ与a、b、c的等式,利用离心率的范围即可求得λ的范围
(λ∈R),将相关点的坐标代入,由向量相等的充要条件,可将N点坐标用λ表示,代入椭圆方程,得λ与a、b、c的等式,利用离心率的范围即可求得λ的范围(2)由(1)知N(
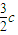 ,
,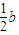 ),再由直线NF2与椭圆联立求得D(0,-b),而点Q的横坐标也已知为
),再由直线NF2与椭圆联立求得D(0,-b),而点Q的横坐标也已知为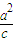 ,将这些点的坐标代入已知
,将这些点的坐标代入已知 =m(
=m(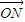 +
+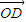 ),即可得m=
),即可得m=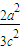 =
=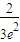 ,Q(
,Q(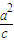 ,-
,-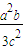 ),从而求得切线NQ的斜率,等于利用导数的几何意义求得的椭圆在点N处的切线斜率,求得椭圆离心率,进而求出m的值
),从而求得切线NQ的斜率,等于利用导数的几何意义求得的椭圆在点N处的切线斜率,求得椭圆离心率,进而求出m的值(3)根据(2)的思路,只需求出直线NF1与椭圆的交点C的横坐标,代入
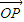 =n(
=n(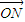 +
+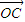 ),得m与离心率的关系,代入求得的离心率即可猜想n值
),得m与离心率的关系,代入求得的离心率即可猜想n值解答:解:(1)设N(x,y)
∵F1(-c,0)F2(c,0),A(0,b),
∴
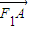 =(c,b),
=(c,b),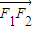 =((2c,0),
=((2c,0),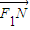 =(x+c,y)
=(x+c,y)∵
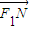 =
=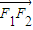 +λ
+λ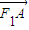 (λ∈R),
(λ∈R),∴(x+c,y)=(2c,0)+λ(c,b),
∴
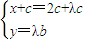
∴
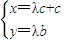 ,
,∵N点在椭圆上,代入椭圆方程
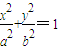
得
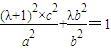
∴
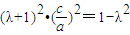 ,显然λ=-1满足等式
,显然λ=-1满足等式若λ≠-1,则
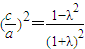
∵椭圆的离心率e=
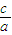 ∈(0,1)
∈(0,1)∴0<
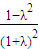 <1
<1解得0<λ<1
∴实数λ的取值范围为(0,1)∪{-1}
(2)∵λ=

∴N(
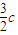 ,
,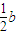 )
)∵直线NF2的方程为y=
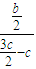 (x-c)
(x-c)即y=
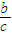 (x-c),∵此直线过点(0,-b)
(x-c),∵此直线过点(0,-b)∴D(0,-b)
假设存在实数m,使
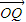 =m(
=m(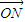 +
+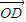 )
)∵Q在右准线x=
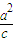 上,∴Q的横坐标为
上,∴Q的横坐标为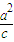 ,设纵坐标为yQ
,设纵坐标为yQ则(
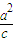 ,yQ)=m[(
,yQ)=m[(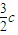 ,
,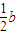 )+(0,-b)]
)+(0,-b)]∴
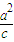 =
=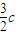 ×m,∴m=
×m,∴m=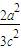 =
=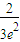 *
*∴yQ=-
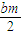 =-
=-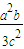
Q(
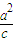 ,-
,-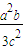 )
)∵直线NQ的斜率为
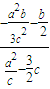 =
=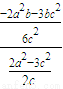 =
=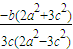 ①
①由
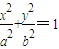 ,得椭圆在第一象限的图象的函数解析式为y=
,得椭圆在第一象限的图象的函数解析式为y=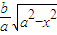
y′=
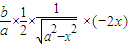 =
=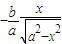
∴y′
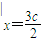 =
=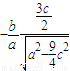 =
=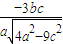
即椭圆切线NQ的斜率为
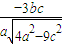 ②
②由①②得
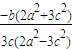 =
=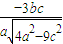
化简得
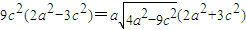
两边同除以a4,得
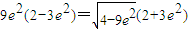
解得e2=

代入*式,得m=
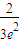 =2
=2故存在实数m=2,使
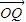 =m(
=m(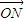 +
+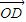 )
)(3)∵N(
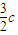 ,
,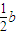 )
)∵直线NF1的方程为y=
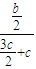 (x+c)
(x+c)即y=
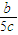 (x+c),代入椭圆方程得(1+
(x+c),代入椭圆方程得(1+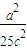 )x2+
)x2+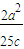 x-
x-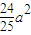 =0
=0∴xC×
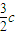 =
=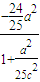
∴xC=
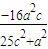 ,
,假设存在实数n,使
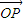 =n(
=n(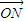 +
+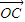 )
)∵P在左准线x=-
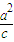 上,∴Q的横坐标为-
上,∴Q的横坐标为-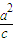 ,设纵坐标为yP
,设纵坐标为yP则(-
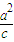 ,yP)=m[(
,yP)=m[(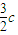 ,
,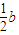 )+(
)+(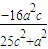 ,yC)]
,yC)]∴-
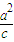 =(
=(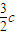 +
+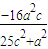 )×m,
)×m,∴m=
 =
=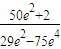
由(2)知e2=

代入上式得:m=14
故猜想存在n=14,使
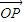 =n(
=n(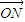 +
+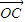 )
)点评:本题考查了椭圆的标准方程及其几何性质,直线与椭圆的位置关系,向量与解析几何的综合运用

练习册系列答案
相关题目