题目内容
已知a、b为异面直线,点A、B在直线a上,点C、D在直线b上,且AC=AD,BC=BD,则直线a、b所成的角为( )
分析:取CD的中点E,连结AE、BE.分别在等腰△ACD与等腰△BCD中证出AE⊥CD、BE⊥CD,从而得出CD⊥平面ABE,得到CD⊥AB,由此即可得到异面直线a、b所成的角大小.
解答:解: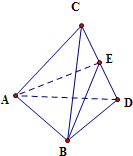 取CD的中点E,连结AE、BE
取CD的中点E,连结AE、BE
∵△ACD中,AC=AD,E为CD中点,∴AE⊥CD
同理可得BE⊥CD
∵AE、BE是平面ABE内的相交直线
∴CD⊥平面ABE
∵AB?平面ABE,∴CD⊥AB
由此可得AB、CD所成的角为直角,即为异面直线a、b所成的角
所以异面直线a、b所成的角等于90°
故选:A
 取CD的中点E,连结AE、BE
取CD的中点E,连结AE、BE∵△ACD中,AC=AD,E为CD中点,∴AE⊥CD
同理可得BE⊥CD
∵AE、BE是平面ABE内的相交直线
∴CD⊥平面ABE
∵AB?平面ABE,∴CD⊥AB
由此可得AB、CD所成的角为直角,即为异面直线a、b所成的角
所以异面直线a、b所成的角等于90°
故选:A
点评:本题给出异面直线满足的条件,求异面直线所成角大小.着重考查了空间线面垂直判定定理、异面直线所成角的定义与求法等知识,属于中档题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目