题目内容
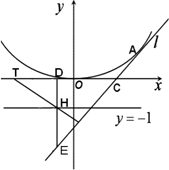
如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.(I)求证:|OC|=|DF|;
(II)试判断直线EF与抛物线的位置关系并说明理由.
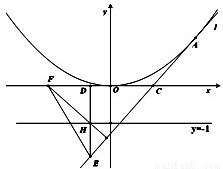
【答案】分析:(I)先利用导数的几何意义,求出过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l的方程,令y=0即可得C点的坐标,再由HF垂直直线l,写出直线HF的方程,令y=0即可得F点的坐标,从而可证|OC|=|DF|
(II)先求出E点的坐标,由(I)知F的坐标,从而写出直线EF的方程,再与抛物线x2=4y联立,证明△=0,即可证明直线EF与抛物线的位置关系为相切
解答:解:(I)∵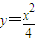 ∴
∴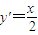 ∴
∴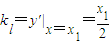
∴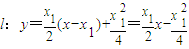
∴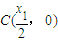
设H(a,-1)∴D(a,0)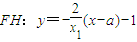 ∴
∴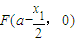
∴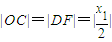
(II)∵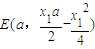 ,
,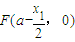
∴
∴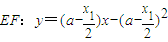
由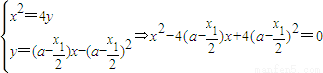
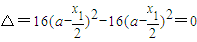
∴直线EF与抛物线相切.
点评:本题考察了直线与抛物线的位置关系,特别注意当直线与抛物线相切时,可利用导数的几何意义,也可联立通过判别式△解决问题
(II)先求出E点的坐标,由(I)知F的坐标,从而写出直线EF的方程,再与抛物线x2=4y联立,证明△=0,即可证明直线EF与抛物线的位置关系为相切
解答:解:(I)∵
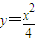 ∴
∴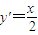 ∴
∴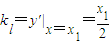
∴
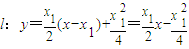
∴
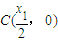
设H(a,-1)∴D(a,0)
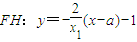 ∴
∴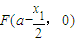
∴
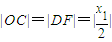
(II)∵
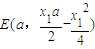 ,
,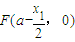
∴

∴
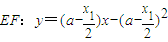
由
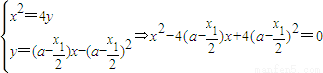
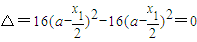
∴直线EF与抛物线相切.
点评:本题考察了直线与抛物线的位置关系,特别注意当直线与抛物线相切时,可利用导数的几何意义,也可联立通过判别式△解决问题

练习册系列答案
相关题目
 (2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.
(2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.