题目内容
17.在△ABC中,已知$\overrightarrow{AB}•\overrightarrow{AC}=2\overrightarrow{AB}•\overrightarrow{BC}$若cosA=$\frac{4}{5}$,则tanB=-$\frac{3}{2}$.分析 设△ABC的三边分别是a,b,c,运用向量数量积的定义和正弦定理,结合同角的平方关系和商数关系,化简即可得到所求值.
解答 解:设△ABC的三边分别是a,b,c,
由$\overrightarrow{AB}•\overrightarrow{AC}=2\overrightarrow{AB}•\overrightarrow{BC}$,可得
cbcosA=-2cacosB,
由正弦定理可得,sinBcosA=-2sinAcosB,
则tanB=$\frac{sinB}{cosB}$=-$\frac{2sinA}{cosA}$=-2tanA,
由cosA=$\frac{4}{5}$,可得sinA=$\sqrt{1-\frac{16}{25}}$=$\frac{3}{5}$,
则tanA=$\frac{sinA}{cosA}$=$\frac{3}{4}$,
即有tanB=-$\frac{3}{2}$.
故答案为:-$\frac{3}{2}$.
点评 本题考查向量的数量积的定义和正弦定理的运用,考查三角函数的化简和求值,属于中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
12.数列{an}前n项和为Sn,a1=1,a2=3,且an+2=|an+1-an|(n∈N*),则S2015=( )
| A. | 1342 | B. | 1344 | C. | 1346 | D. | 1348 |
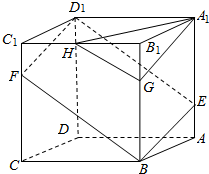 如图.已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1.H是B1C1的中点.
如图.已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1.H是B1C1的中点.