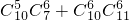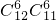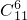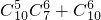题目内容
浙江省新课程自选模块考试试题中共有18道题,考生要从中任选6道题进行解答,现有两位考生,其中考生甲一定不选第2,6,9,13,14,17,18题,考生乙一定不选第7,9,13,14,17,18题,若考生甲与乙选取的6道题都不相同,则满足要求的选法种数共有( )A.

B.

C.

D.

【答案】分析:先将问题简化为“从13道题中选6道,甲不选2,6,乙不选7”,再利用分类计数原理,将问题按甲选不选7题分成两类计数,最后求两类计数结果之和;在每一类的计数中可利用分步计数原理,第一步由甲选,第二步由乙选,最后将两步结果相乘即可
解答:解:注意到有5道题甲乙都不能选,故此问题相当于从13道题中选6道,甲不选2,6,乙不选7
分两类来计数:
第一类:甲选了第7题:则第一步,甲只需在剩下的10道题中选5道即可,共有 种选法;第二步,乙则只需从甲选后剩下的7道题中任选6道,共有
种选法;第二步,乙则只需从甲选后剩下的7道题中任选6道,共有 种选法;
种选法;
故由分步计数原理,共有 种不同选法;
种不同选法;
第二类:甲没选第7题:则第一步,甲只需从剩下的10题中任选6题,共有 种选法,第二步,乙只能选剩下的6道题,有一种选法;
种选法,第二步,乙只能选剩下的6道题,有一种选法;
故由分步计数原理,共有 种不同选法;
种不同选法;
由分类计数原理,满足要求的选法种数共有 个
个
故选D
点评:本题主要考查了分类计数原理和分步计数原理的运用,排列组合计数公式的运用,分类讨论的思想方法和转化化归的思想方法,属基础题
解答:解:注意到有5道题甲乙都不能选,故此问题相当于从13道题中选6道,甲不选2,6,乙不选7
分两类来计数:
第一类:甲选了第7题:则第一步,甲只需在剩下的10道题中选5道即可,共有
 种选法;第二步,乙则只需从甲选后剩下的7道题中任选6道,共有
种选法;第二步,乙则只需从甲选后剩下的7道题中任选6道,共有 种选法;
种选法;故由分步计数原理,共有
 种不同选法;
种不同选法;第二类:甲没选第7题:则第一步,甲只需从剩下的10题中任选6题,共有
 种选法,第二步,乙只能选剩下的6道题,有一种选法;
种选法,第二步,乙只能选剩下的6道题,有一种选法;故由分步计数原理,共有
 种不同选法;
种不同选法;由分类计数原理,满足要求的选法种数共有
 个
个故选D
点评:本题主要考查了分类计数原理和分步计数原理的运用,排列组合计数公式的运用,分类讨论的思想方法和转化化归的思想方法,属基础题

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目