题目内容
已知圆的极坐标方程为 ,则该圆的圆心到直线
,则该圆的圆心到直线 的距离是 .
的距离是 .
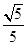
解析试题分析:解:由ρ=2cosθ,化为直角坐标方程为x2+y2-2x=0,其圆心是A(1,0),由ρsinθ+2ρcosθ=1得:化为直角坐标方程为2x+y-1=0,由点到直线的距离公式,得d= ,故可知答案为
,故可知答案为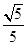
考点:圆和直线的极坐标方程
点评:本小题主要考查圆和直线的极坐标方程与直角坐标方程的互化,以及利用圆的几何性质计算圆心到直线的距等基本方法,属于基础题

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
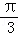 ),(4,
),(4, ),则△AOB(其中O为极点)的面积为 .
),则△AOB(其中O为极点)的面积为 . 的圆心极坐标为 .
的圆心极坐标为 .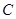 :
: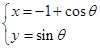
 为参数)和直线:
为参数)和直线: (为参数), 则曲线
(为参数), 则曲线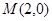 的直线
的直线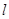 与极轴的夹角
与极轴的夹角 ,若将
,若将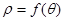 的形式,则
的形式,则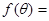

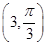 、
、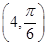 ,则
,则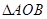 (其中O为极点)的面积为
(其中O为极点)的面积为 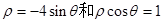 相交于点A、B,则|AB|= 。
相交于点A、B,则|AB|= 。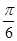 和sinθ=
和sinθ= ; ②θ=
; ②θ=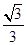 ; ③ρ2-9=0和ρ= 3;
; ③ρ2-9=0和ρ= 3; 和
和 . 其中表示相同曲线的组数为 .
. 其中表示相同曲线的组数为 .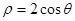 的圆心到直线
的圆心到直线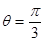
 的距离是
的距离是 ;
;