题目内容
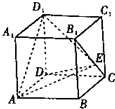 (2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为
(2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为| 1 |
| 6 |
| 1 |
| 6 |
分析:将三棱锥A-DED1选择△ADD1为底面,E为顶点,进行等体积转化V A-DED1=V E-ADD1后体积易求
解答:解:将三棱锥A-DED1选择△ADD1为底面,E为顶点,则V A-DED1=V E-ADD1,
其中S△ADD1=
SA1D1DA=
,E到底面ADD1的距离等于棱长1,
故V=
•
•1=
.
故答案为:
其中S△ADD1=
| 1 |
| 2 |
| 1 |
| 2 |
故V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题考查了三棱柱体积的计算,等体积转化法是常常需要优先考虑的策略.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
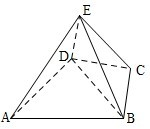 (2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(2012•山东)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD. (2012•山东)如图,椭圆
(2012•山东)如图,椭圆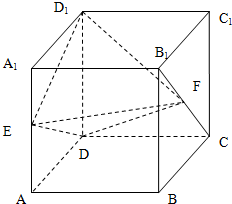 (2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为
(2012•山东)如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为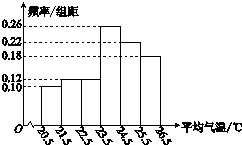 (2012•山东)如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为
(2012•山东)如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为