题目内容
已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.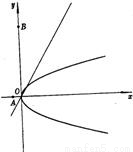
【答案】分析:先设出抛物线的标准方程和直线l的方程,根据A'、B'分别是A、B关于l的对称点,进而可知A'A⊥l,进而可得直线A'A的方程,把两直线方程联立求得交点M的坐标,进而根据M为AA'的中点,求得A'点的坐标和B'的坐标,分别代入抛物线方程求得p的表达式,最后联立求得k,进而求得p,则直线和抛物线的方程可得.
解答: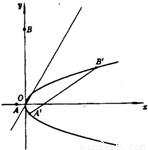 解:依题设抛物线C的方程可写为
解:依题设抛物线C的方程可写为
y2=2px(p>0),
且x轴和y轴不是所求直线,又l过原点,因而可设l的方程为
y=kx(k≠0).①
设A'、B'分别是A、B关于l的对称点,因而A'A⊥l,直线A'A的方程为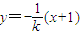 ②
②
由①、②联立解得AA'与l的交点M的坐标为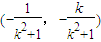 .
.
又M为AA'的中点,从而点A'的坐标为
xA'=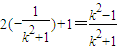 ,
,
yA'= .③
.③
同理得点B'的坐标为
xB'=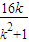 ,yB'=
,yB'=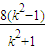 .④
.④
又A'、B'均在抛物线y2=2px(p>0)上,由③得 ,由此知k≠±1,
,由此知k≠±1,
即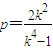 ⑤
⑤
同理由④得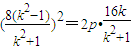 .
.
即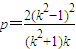 .
.
从而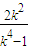 =
=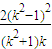 ,
,
整理得k2-k-1=0.
解得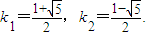
但当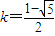 时,由③知
时,由③知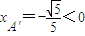 ,
,
这与A'在抛物线y2=2px(p>0)上矛盾,故舍去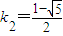 .
.
设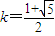 ,则直线l的方程为
,则直线l的方程为 .
.
将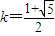 代入⑤,求得
代入⑤,求得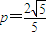 .
.
所以直线方程为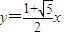 .
.
抛物线方程为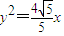 .
.
点评:本小题考查直线与抛物线的基本概念和性质,解析几何的基本思想方法以及综合运用知识解决问题的能力.
解答:
 解:依题设抛物线C的方程可写为
解:依题设抛物线C的方程可写为y2=2px(p>0),
且x轴和y轴不是所求直线,又l过原点,因而可设l的方程为
y=kx(k≠0).①
设A'、B'分别是A、B关于l的对称点,因而A'A⊥l,直线A'A的方程为
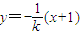 ②
②由①、②联立解得AA'与l的交点M的坐标为
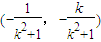 .
.又M为AA'的中点,从而点A'的坐标为
xA'=
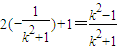 ,
,yA'=
 .③
.③同理得点B'的坐标为
xB'=
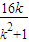 ,yB'=
,yB'=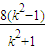 .④
.④又A'、B'均在抛物线y2=2px(p>0)上,由③得
 ,由此知k≠±1,
,由此知k≠±1,即
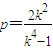 ⑤
⑤同理由④得
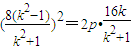 .
.即
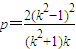 .
.从而
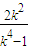 =
=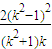 ,
,整理得k2-k-1=0.
解得
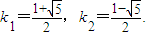
但当
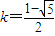 时,由③知
时,由③知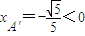 ,
,这与A'在抛物线y2=2px(p>0)上矛盾,故舍去
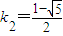 .
.设
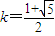 ,则直线l的方程为
,则直线l的方程为 .
.将
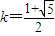 代入⑤,求得
代入⑤,求得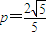 .
.所以直线方程为
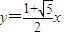 .
.抛物线方程为
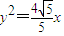 .
.点评:本小题考查直线与抛物线的基本概念和性质,解析几何的基本思想方法以及综合运用知识解决问题的能力.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
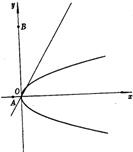 已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.
已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.