设实数a.b满足2a+b=9．(1)若|9-b|+|a|＜3.求a的取值范围,(2)求|3a-b|+|a-2b|的最小值．题目和参考答案——青夏教育精英家教网—

题目内容

7．设实数a，b满足2a+b=9．
（1）若|9-b|+|a|＜3，求a的取值范围；
（2）求|3a-b|+|a-2b|的最小值．

分析（1）由条件可得3|a|＜3，利用绝对值不等式的解法，求得a的范围．
（2）要求的式子即|5a-9|+|5a-18|，再利用绝对值三角不等式求得它的最小值．

解答解：实数a，b满足2a+b=9．
（1）∵|9-b|+|a|=|2a|+|a|=3|a|＜3，∴|a|＜1，∴-1＜a＜1，故要求的a的取值范围为（-1，1）．
（2）求|3a-b|+|a-2b|=|3a-（9-2a）|+|a-2（9-2a）|=|5a-9|+|5a-18|≥|（5a-9）-（5a-18）|=9，
故|3a-b|+|a-2b|的最小值为9．

点评本题主要考查绝对值不等式的解法，绝对值三角不等式的应用，属于基础题．

练习册系列答案

相关题目

17．设f（x）=2^x+3x-8，则方程f（x）=0的根落在区间（　　）

18．抛物线y²=2px的准线方程是x=-2，则p的值是（　　）

15．若双曲线C与椭圆x²+4y²=64有相同的焦点，它的一条渐近线方程是$x+\sqrt{3}y=0$，求双曲线C的方程．

2．已知x∈R，符号[x]表示不超过x的最大整数，若函数f（x）=$\frac{[x]}{x}$（x＞0），则给出以下四个结论正确的是（　　）

	A．	函数f（x）的值域为（0，1]
	B．	函数f（x）没有零点
	C．	函数f（x）是（0，+∞）上的减函数
	D．	函数g（x）=f（x）-a有且仅有3个零点时$\frac{3}{4}$＜a≤$\frac{4}{5}$

12．为了检测某种产品的质量，抽取了一个容量为100的样本，数据的分组数如下：
[10.75，10.85）3；[10.85，10.95）9；[10.95，11.05）13；
[11.05，11.15）16；[11.15，11.25）26；[11.25，11.35）20；
[11.35，11.45）7；[11.45，11.55）4；[11.55，11.65）2；
估计数据落在[10.95，11.35）范围内的频率为（　　）

19．

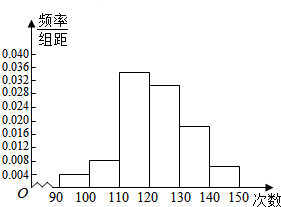为了了解高一年级学生的体能情况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图所示），图中从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组的频数为12．则样本容量为150．

16．设数列{a_n}的前n项和为S_n，且满足S_n=2a_n-1（n∈N*）．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）求数列$\left\{{\frac{2n-1}{a_n}}\right\}$的前n项和T_n；
（Ⅲ）数列{b_n}满足b_n+1=a_n+b_n（n∈N*），且b₁=3．若不等式${log_2}（{b_n}-2）＜\frac{3}{16}{n^2}+t$对任意n∈N^*恒成立，求实数t的取值范围．

17．

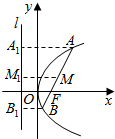如图：AB是抛物线y²=2px（p＞0）过焦点F的一条弦，设A（x₁，y₁），B（x₂，y₂），AB的中点M（x₀，y₀），相应的准线为l．
证明：
（1）以AB为直径的圆必与准线l相切；
（2）|AB|=2（x₀+$\frac{p}{2}$）（焦点弦长与中点关系）；
（3）|AB|=x₁+x₂+p；
（4）x₁•x₂=$\frac{{p}^{2}}{4}$，y₁•y₂=-p²．

试题分类