题目内容
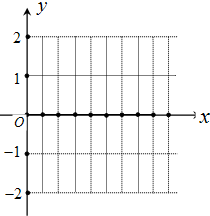 定义运算a⊕b=a2+2ab-b2,记函数f(x)=sinx⊕cosx
定义运算a⊕b=a2+2ab-b2,记函数f(x)=sinx⊕cosx
(Ⅰ)已知 ,且
,且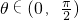 ,求f(θ)的值;
,求f(θ)的值;
(Ⅱ)在给定的直角坐标系中,用“五点法”作出函数f(x)在一个周期内的简图;
(Ⅲ)求函数f(x)的对称中心、最大值及相应的x值.
解:(Ⅰ)由题意可得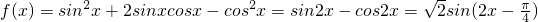 -----(2分)
-----(2分)
∴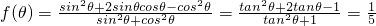 --------(5分)
--------(5分)
(Ⅱ)∵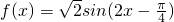 ,运用“五点法”先列表后描点连线,
,运用“五点法”先列表后描点连线,
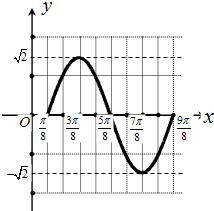 作出函数f(x)在一个周期内的图象如下,
作出函数f(x)在一个周期内的图象如下,
(10分)
(Ⅲ)∵函数y=sinx的对称中心为(kπ,0)(k∈Z),且当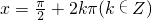 时,ymax=1
时,ymax=1
令 ,由
,由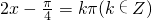 ,解得
,解得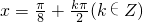
∴函数f(x)的对称中心为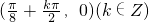 -------(12分)
-------(12分)
当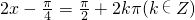 ,即
,即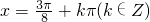 ,
,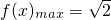 -------(14分)
-------(14分)
分析:(Ⅰ)由新定义可得函数的解析式,代入化切后计算可得答案;(Ⅱ)由五点法,列表、描点,连线可得图象;(Ⅲ)函数y=sinx的对称中心为(kπ,0)(k∈Z),且当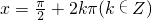 时,ymax=1,把
时,ymax=1,把 整体代入解之可得答案.
整体代入解之可得答案.
点评:本题考查五点作图,涉及同角三角函数的基本关系和正弦函数的对称性,属中档题.
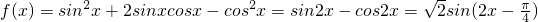 -----(2分)
-----(2分)∴
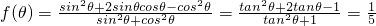 --------(5分)
--------(5分)(Ⅱ)∵
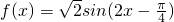 ,运用“五点法”先列表后描点连线,
,运用“五点法”先列表后描点连线,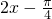 | 0 |  | π |  | 2π |
| x |  |  |  |  |  |
 | 0 |  | 0 |  | 0 |
 作出函数f(x)在一个周期内的图象如下,
作出函数f(x)在一个周期内的图象如下,(10分)
(Ⅲ)∵函数y=sinx的对称中心为(kπ,0)(k∈Z),且当
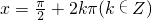 时,ymax=1
时,ymax=1令
 ,由
,由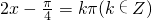 ,解得
,解得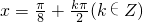
∴函数f(x)的对称中心为
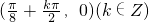 -------(12分)
-------(12分)当
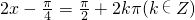 ,即
,即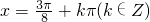 ,
,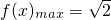 -------(14分)
-------(14分)分析:(Ⅰ)由新定义可得函数的解析式,代入化切后计算可得答案;(Ⅱ)由五点法,列表、描点,连线可得图象;(Ⅲ)函数y=sinx的对称中心为(kπ,0)(k∈Z),且当
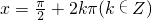 时,ymax=1,把
时,ymax=1,把 整体代入解之可得答案.
整体代入解之可得答案.点评:本题考查五点作图,涉及同角三角函数的基本关系和正弦函数的对称性,属中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
定义运算a⊕b=a2-ab-b2,则sin
⊕cos
=( )
| π |
| 6 |
| π |
| 6 |
A、-
| ||||||
B、-
| ||||||
C、1+
| ||||||
D、1-
|