题目内容
【题目】如下图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.

(1)证明:![]() ;
;
(2)是否存在实数![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出实数
?若存在,求出实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)证明见解析;(2)存在,![]()
【解析】
(1)因为平面![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() ,根据勾股定理得:
,根据勾股定理得:![]() ,又因为
,又因为 ![]() ,所以根据勾股定理逆定理得:
,所以根据勾股定理逆定理得:![]() ,故
,故![]() ,
,![]() 平面
平面![]() ,故:
,故:![]()
(2)通过建立空间直角坐标系![]() ,通过向量法即可得出
,通过向量法即可得出![]() 的值.
的值.
(1)证明:过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴四边形![]() 为正方形,且
为正方形,且![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,
,
∴![]() ,即
,即![]() .
.
又∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() .
.
∴![]() 平面
平面![]() ,又因为
,又因为![]() 面
面![]() ∴
∴![]() .
.
又∵![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ∴
∴![]() 平面
平面![]() ,又∵
,又∵![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)解:由(1)知![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() ,又∵
,又∵![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在的直线为坐标轴建立如图所示的空间直角坐标系
所在的直线为坐标轴建立如图所示的空间直角坐标系![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
假设存在实数![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,则
,则![]() ,
,
因为点![]() 在棱
在棱![]() 上,∴
上,∴![]() .
.
设![]() ,由
,由![]() ,得
,得![]() ,
,
∴![]() ,则
,则![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由 ,所以
,所以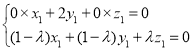 ,令
,令![]() ,则
,则![]()
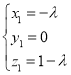
故平面![]() 的一个法向量为
的一个法向量为![]() .
.
∴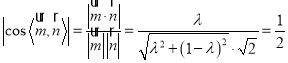 ,
,
解得![]() ,
,
∴存在实数![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】新高考,取消文理科,实行“![]() ”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在
”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在![]() 称为中青年,年龄在
称为中青年,年龄在![]() 称为中老年),并把调查结果制成下表:
称为中老年),并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 15 | 10 | 10 | 5 | 5 |
了解 | 4 | 12 | 6 | 5 | 2 | 1 |
(1)分别估计中青年和中老年对新高考了解的概率;
(2)请根据上表完成下面![]() 列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
了解新高考 | 不了解新高考 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
附: .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)若从年龄在![]() 的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为
的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为![]() ,求
,求![]() 的分布列以及
的分布列以及![]() .
.
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
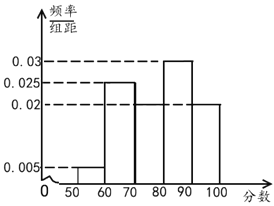
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |