题目内容
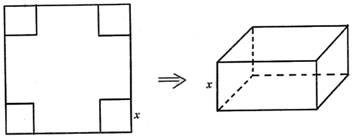
把边长为60cm的正方形铁皮的四角切去边长为x cm的相等的正方形,然后折成一个高度为x cm的无盖的长方体的盒子,要求长方体的高度与底面边长的比值不超过常数k(k>0),问x取何值时,盒子的容积最大,最大容积是多少?
解:设长方体高为x cm,则底面边长为(60-2x)cm,(0<x<30)
长方体容积V=V(x)=x(60-2x)2=4x(x-30)2(单位:cm3)
∵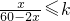 ,∴
,∴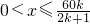 .
.
即函数定义域为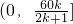 ,
,
V′(x)=4(x-30)2+8x(x-30)=4(x-30)(3x-30)=12(x-30)(x-10)
令V′(x)=0,解得x=10,x=30(不合题意舍去),于是
①当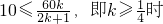 ,
,
在x=10时,V取得最大值为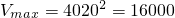
②当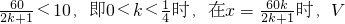 取得最大值
取得最大值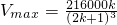
分析:设长方体高为x cm,求题意求出底面边长,并注明x的范围,再求出长方体容积V=V(x),再由条件求出函数的定义域,再求出V′(x),求出临界点、列表格,判断出函数的单调性,再由表格对k进行分类,分别求出V(x)的最大值和对应的x的值.
点评:本题考查了函数的实际应用,利用导数来研究函数的单调性、最值问题等,注意自变量的实际意义,考查了分类讨论思想.
长方体容积V=V(x)=x(60-2x)2=4x(x-30)2(单位:cm3)
∵
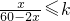 ,∴
,∴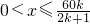 .
.即函数定义域为
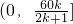 ,
,V′(x)=4(x-30)2+8x(x-30)=4(x-30)(3x-30)=12(x-30)(x-10)
令V′(x)=0,解得x=10,x=30(不合题意舍去),于是
| x | (0,10) | 10 | (10,30) |
| V′(x) | + | 0 | - |
| V(x) | ↑ | ↓ |
①当
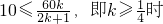 ,
,在x=10时,V取得最大值为
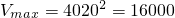
②当
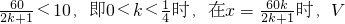 取得最大值
取得最大值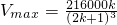
分析:设长方体高为x cm,求题意求出底面边长,并注明x的范围,再求出长方体容积V=V(x),再由条件求出函数的定义域,再求出V′(x),求出临界点、列表格,判断出函数的单调性,再由表格对k进行分类,分别求出V(x)的最大值和对应的x的值.
点评:本题考查了函数的实际应用,利用导数来研究函数的单调性、最值问题等,注意自变量的实际意义,考查了分类讨论思想.

练习册系列答案
相关题目