题目内容
6．函数f（x）=xex在点（1，f（1））处的切线方程是y=2ex-e．分析 求出函数的导数，求得切线的斜率和切点，由点斜式方程即可得到切线方程．
解答 解：函数f（x）=xex的导数为f′（x）=ex+xex，
在点（1，f（1））处的切线斜率为k=2e，
切点为（1，e），
则有在点（1，f（1））处的切线方程为y-e=2e（x-1），
即为y=2ex-e．
故答案为：y=2ex-e．
点评 本题考查导数的运用：求切线方程，主要考查导数的几何意义：函数在某点处的导数即为曲线在该点处切线的斜率，正确求导和运用点斜式方程是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．已知双曲线kx2-y2=1的一条渐近线与直线2x+y+1=0垂直，则双曲线的离心率是（ ）
| A． | $\frac{\sqrt{5}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{3}$ | D． | $\sqrt{5}$ |
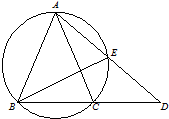如图，⊙O是△ABC的外接圆，AC=CD，AB=AC，延长BC到点D，连结AD交⊙O于点E，连结BE，若∠D=40°，则∠ABE的大小为40°．
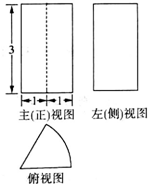某圆柱切割获得的几何体的三视图如图所示，其中俯视图是中心角为$\frac{π}{3}$的扇形，则该几何体的体积为2π．
18．在△ABC 中，若A=$\frac{π}{3}$，cosB=$\frac{{\sqrt{6}}}{3}$，BC=6，则 AC=（ ）
| A． | 4$\sqrt{2}$ | B． | 4 | C． | 2$\sqrt{3}$ | D． | $\frac{{4\sqrt{3}}}{3}$ |