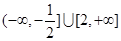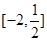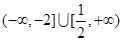题目内容
在平面直角坐标系中,若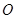 为坐标原点,则
为坐标原点,则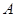 、
、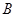 、
、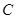 三点在同一直线上的等价于存在唯一的实数
三点在同一直线上的等价于存在唯一的实数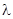 ,使得
,使得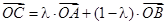 成立,此时称实数
成立,此时称实数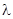 为“向量
为“向量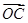 关于
关于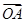 和
和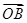 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知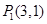 、
、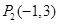 ,且向量
,且向量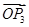 与向量
与向量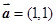 垂直,则“向量
垂直,则“向量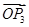 关于
关于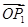 和
和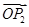 的终点共线分解系数”为_________________.
的终点共线分解系数”为_________________.
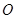 为坐标原点,则
为坐标原点,则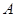 、
、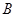 、
、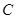 三点在同一直线上的等价于存在唯一的实数
三点在同一直线上的等价于存在唯一的实数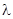 ,使得
,使得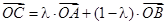 成立,此时称实数
成立,此时称实数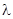 为“向量
为“向量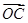 关于
关于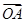 和
和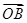 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知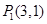 、
、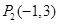 ,且向量
,且向量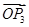 与向量
与向量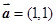 垂直,则“向量
垂直,则“向量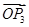 关于
关于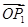 和
和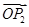 的终点共线分解系数”为_________________.
的终点共线分解系数”为_________________.-1
试题分析:向量
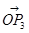 与向量
与向量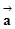 =(1,1)垂直,则由两向量垂直数量积为零,我们可设出向量
=(1,1)垂直,则由两向量垂直数量积为零,我们可设出向量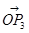 的坐标,然后根据
的坐标,然后根据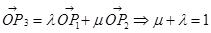 ,易P1(3,1)、P2(-1,3)的坐标,我们可以构造一个关于λ的方程组,解方程组即可求出λ的值.得(t,-t)=λ(1,3)+(1-λ)(-1,3)=(4λ-1,3-2λ),4λ-1="t," 3-2λ=-t,解得两式相加得2λ+2=0,∴λ=-1.故答案为-1.
,易P1(3,1)、P2(-1,3)的坐标,我们可以构造一个关于λ的方程组,解方程组即可求出λ的值.得(t,-t)=λ(1,3)+(1-λ)(-1,3)=(4λ-1,3-2λ),4λ-1="t," 3-2λ=-t,解得两式相加得2λ+2=0,∴λ=-1.故答案为-1.点评:若A、B、P三点共线,O为直线外一点,则
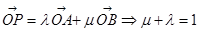 ,且λ+μ=1,反之也成立,这是三点共线在向量中最常用的证明方法和性质,大家一定要熟练掌握.
,且λ+μ=1,反之也成立,这是三点共线在向量中最常用的证明方法和性质,大家一定要熟练掌握.
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
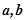 的夹角为
的夹角为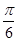 ,且
,且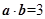 ,
,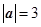 ,则
,则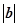 等于( )
等于( )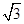
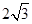
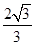
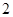
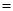
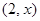 , b
, b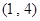 ,若a⊥b,则实数
,若a⊥b,则实数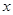 的值为
的值为
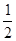
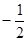
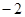
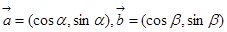 ,其中
,其中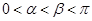 .
.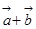 与
与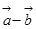 互相垂直;
互相垂直; 与
与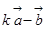 (
(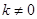 )的长度相等,求
)的长度相等,求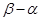 .
.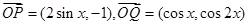 ,定义函数
,定义函数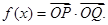
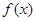 的表达式,并指出其最大最小值;
的表达式,并指出其最大最小值;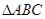 中,角A,B,C的对边分别为a,b,c,且
中,角A,B,C的对边分别为a,b,c,且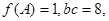 求
求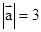 ,
,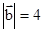 ,且(
,且(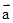 +k
+k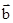 )⊥(
)⊥( k
k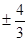
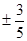
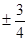
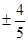
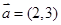 ,
,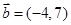 ,则
,则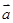 在
在 方向上的投影为( )
方向上的投影为( )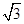
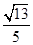
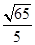
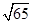
 是平面上的两个向量,若向量
是平面上的两个向量,若向量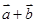 与
与 相互垂直,
相互垂直,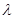 的值;
的值;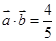 ,且
,且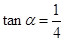 ,求
,求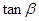 的值.
的值.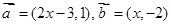 ,若
,若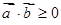 ,则实数
,则实数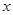 的取值范围是( )
的取值范围是( )