题目内容
已知复数z=1-sinθ+icosθ(
<θ<π),求z的共轭复数
的辐角主值.
| π |
| 2 |
. |
| z |
分析:利用三角函数的倍角公式和诱导公式进行计算并符合辐角主值的范围即可求出答案.
解答:解:z=1+cos(
+θ)+isin(
+θ)=2cos2
+2isin
cos
=2cos
(cos
+isin
).
当
<θ<π时,
<
-
<
.
∴
=-2cos
(-cos
+isin
)=-2cos(
+
)(cos(
-
)+isin(
-
)).
∴辐角主值为
-
.
| π |
| 2 |
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
=2cos
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
当
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| θ |
| 2 |
| π |
| 2 |
∴
. |
| z |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| π |
| 4 |
| θ |
| 2 |
| 3π |
| 4 |
| θ |
| 2 |
| 3π |
| 4 |
| θ |
| 2 |
∴辐角主值为
| 3π |
| 4 |
| θ |
| 2 |
点评:此题考查了复数的三角形式的共轭复数及辐角主值,熟练利用三角函数的倍角公式和诱导公式进行计算并知道辐角主值的范围是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知复数z=1-i,则
=( )
| z2-2z |
| z-1 |
| A、2i | B、-2i | C、2 | D、-2 |
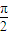 <θ<π),求z的共轭复数
<θ<π),求z的共轭复数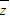 的辐角主值.
的辐角主值.