题目内容
某校高三年级一次数学考试后，为了解学生的数学学习情况，随机抽取
名学生的数学成绩，制成表所示的频率分布表.
（1）求
、
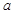、的值；
（2）若从第三、四、五组中用分层抽样方法抽取
名学生，并在这名学生中随机抽取
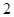名学生与张老师面谈，求第三组中至少有
名学生与张老师面谈的概率
名学生的数学成绩，制成表所示的频率分布表.| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  |  |  |
| 第二组 |  | |  |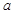
| 第三组 |  |  |  |
| 第四组 |  |  | |
| 第五组 |  |  |  |
| 合计 | |  | |
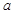、、的值；（2）若从第三、四、五组中用分层抽样方法抽取
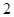名学生，并在这名学生中随机抽取名学生与张老师面谈，求第三组中至少有名学生与张老师面谈的概率（1）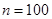
，
，
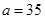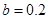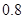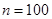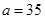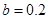；（2）
.
，，；（2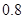）.试题分析：（1）先根据相应组的频数除以样本总容量等于相应组的频率列式求出
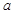、、的值；（2）先利用分成抽样的方法确定从第三、四、五组抽取的人数，并将从每组抽取的人进行编号，利用列举法将所有的基本事件列举出，并确定基本事件总数，然后确定问题中设计事件的基本事件及其数目，利用古典概型的概率计算公式求出相应事件的概率.试题解析：（1）依题意，得
，
，
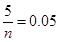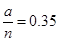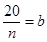，解得
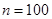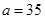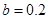，，；（2）因为第三、四、五组共有
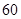名学生，用分层抽样的方法抽取名学生，则第三、四、五组分别抽取
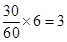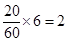名，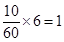
名，
名.第三组的
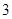名学生记为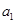
、
、
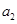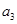，第四组的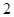名学生记为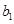
、
，第五组的名学生记为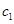
，则从
名学生中随机抽取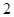名，共有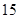
种不同取法，具体如下：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
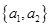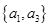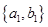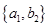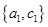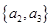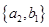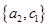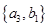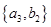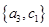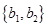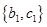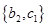，其中第三组的
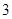名学生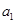、、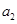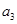没有一名学生被抽取的情况有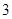种，具体如下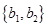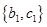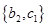：、、，故第三组中至少有
名学生与张老师面谈的概率为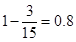
.
练习册系列答案
阅读快车系列答案
相关题目
＝40；
与
分别表示图甲中各组的组中值及频率） 
的范围，但他俩坚称没喝那么多，是测试仪不准，交警大队队长决定在被酒精测试仪测得酒精浓度属于70～90
为吴、李两位先生被抽中的人数，求
＝40
三所不同的中学抽取60名教师进行调查.已知
学校中应抽取的人数为（ ）.