题目内容
9.现定义an=5n+($\frac{1}{5}$)n,其中n∈{$\frac{1}{10}$,$\frac{1}{5}$,$\frac{1}{2}$,1},则an取最小值时,n的值为( )| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 对数列函数f(n)=5n+($\frac{1}{5}$)n求导数,由导函数的符号判断数列an=5n+($\frac{1}{5}$)n为递增数列,由此可得an取最小值时n的值.
解答 解:∵an=5n+($\frac{1}{5}$)n,
令f(n)=5n+($\frac{1}{5}$)n,
∴${f}^{′}(n)=n•{5}^{n-1}+n•(\frac{1}{5})^{n-1}>0$(n>0),
∴数列an=5n+($\frac{1}{5}$)n为递增数列,
则当n∈{$\frac{1}{10}$,$\frac{1}{5}$,$\frac{1}{2}$,1},且an取最小值时,n的值为$\frac{1}{10}$.
故选:A.
点评 本题考查了数列递推式,考查了数列的函数特性,训练了利用导数研究函数的单调性,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设两个向量$\overrightarrow a=(λ+2,{λ^2}-{cos^2}α)$和$\overrightarrow b=({m,\frac{m}{2}+sinα})$,其中λ,m,α为实数,若$\overrightarrow a=2\overrightarrow b$,则λ的取值范围是( )
| A. | $[{-\frac{3}{2},2}]$ | B. | $[{-2,\frac{3}{2}}]$ | C. | $[{-2,-\frac{3}{2}}]$ | D. | $[{\frac{3}{2},2}]$ |
1.若(9x-$\frac{1}{3\sqrt{x}}$)n(n∈N*)的展开式中第2项的二项式系数为9,则其展开式中的常数项为( )
| A. | -84 | B. | -252 | C. | 252 | D. | 84 |
18.已知a,b∈R,则“a>b”是“a>b-1”成立的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
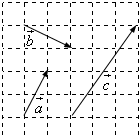 如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则$\frac{x}{y}$=$\frac{11}{2}$.
如图,在6×6的方格纸中,若起点和终点均在格点的向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{c}$=x$\overrightarrow{a}$+y$\overrightarrow{b}$(x,y∈R),则$\frac{x}{y}$=$\frac{11}{2}$. 在
在 上的导函数为
上的导函数为 ,若
,若 恒成立,且
恒成立,且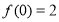 ,则不等式
,则不等式 的解集是( )
的解集是( ) B.
B.
 D.
D.