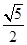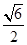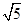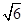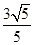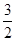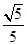题目内容
已知双曲线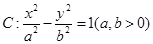 的左、右焦点分别为
的左、右焦点分别为
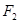 ,过
,过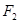 作双曲线
作双曲线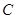 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为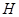 ,若
,若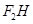 的中点
的中点 在双曲线
在双曲线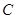 上,则双曲线
上,则双曲线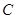 的离心率为( )
的离心率为( )
A. | B.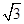 | C.2 | D.3 |
A
解析试题分析:由题意可知,一渐近线方程为  ,则
,则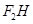 的方程为 y-0=k(x-c),代入渐近线方程
的方程为 y-0=k(x-c),代入渐近线方程 可得
可得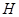 的坐标为
的坐标为 ,故
,故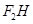 的中点
的中点 ,根据中点
,根据中点 在双曲线
在双曲线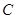 上,∴
上,∴ ,解得
,解得 ,故
,故  ,本题求出
,本题求出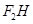 的中点
的中点 的坐标是解题的关键.
的坐标是解题的关键.
考点:双曲线的简单性质.

练习册系列答案
相关题目
动圆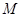 经过双曲线
经过双曲线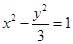 左焦点且与直线
左焦点且与直线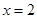 相切,则圆心
相切,则圆心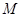 的轨迹方程是( )
的轨迹方程是( )
A. | B.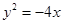 | C. | D.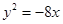 |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A.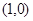 | B.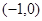 | C.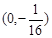 | D.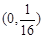 |
已知双曲线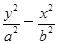 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.y=± x x | B.y=± x x | C.y=±2x | D.y=± x x |
已知点A(2,1),抛物线y2=4x的焦点是F,若抛物线上存在一点P,使得|PA|+|PF|最小,则P点的坐标为( )
| A.(2,1) | B.(1,1) | C.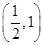 | D.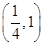 |
双曲线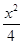 -y2=1的渐近线方程为( )
-y2=1的渐近线方程为( )
| A.x=±2x | B.x=±4x |
C.y=±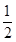 x x | D.y=±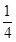 x x |
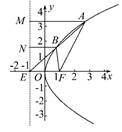
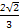
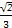


 =1(a>0,b>0)右支上的一点P(x0,y0)到左焦点的距离与到右焦点的距离之差为2
=1(a>0,b>0)右支上的一点P(x0,y0)到左焦点的距离与到右焦点的距离之差为2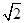 ,且到两条渐近线的距离之积为
,且到两条渐近线的距离之积为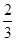 ,则双曲线的离心率为( )
,则双曲线的离心率为( )