题目内容
设直线
与圆
相交于
，
两点，且弦
的长为
，则实数
的值是 .
解析试题分析：由圆的标准方程找出圆心坐标和半径r，然后利用点到直线的距离公式表示出圆心到已知直线的距离d，再由弦AB的长，利用垂径定理及勾股定理列出关于m的方程，求出方程的解即可得到m的值。由圆的方程，得到圆心坐标为（1，2），半径r=2，∵圆心到直线的距离d=
考点：直线与圆的位置关系
点评:此题考查了直线与圆相交的性质，涉及的知识有：圆的标准方程，点到直线的距离公式，垂径定理，以及勾股定理的运用，当直线与圆相交时，常常根据垂径定理由垂直得中点，进而再由弦心距，圆的半径及弦长的一半，利用勾股定理解决问题
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
被圆
截得的弦长为_______________.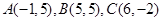
的圆的方程是 . 
与圆
的公共弦所在直线的方程为 
.
，过点
作直线交圆C于
两点，
面积的最大值为__________．
且与直线
相切的圆的方程是 ．
与直线
相切，且圆D与圆C关于直线
对称，则圆D的方程是___________。
相切，若切点在第二象限，则该直线的方程为 ．
内点
作圆的两条互相垂直的弦
和
，则
的最大值为 .