题目内容
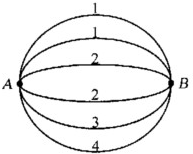 如图,A,B两点之间有6条网线连接,每条网线能通过的最大信息量分别为1,1,2,2,3,4.从中任取三条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息量之和为ξ.
如图,A,B两点之间有6条网线连接,每条网线能通过的最大信息量分别为1,1,2,2,3,4.从中任取三条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息量之和为ξ.
(1)当ξ≥6时,则保证线路信息畅通,求线路信息畅通的概率;
(2)求ξ的分布列和数学期望.
解:(1)∵1+1+4=1+2+3=6,∴P(ξ=6)=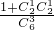 =
=
∵1+2+4=2+2+3=7,∴P(ξ=7)=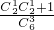 =
=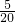 =
= ,
,
∵2+2+4=1+3+4=8,∴P(ξ=8)=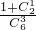 =
= ,
,
∵2+3+4=9,∴P(ξ=9)=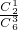 =
=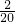 =
= ,
,
∴线路信息畅通的概率是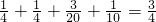 .
.
(2)ξ=4,5,6,7,8,9
∵1+1+2=4,∴P(ξ=4)=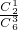 =
=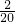 =
= ,
,
∵1+1+3=1+2+2=5,∴P(ξ=5)=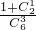 =
= ,
,
ξ的分布列为
∴线路通过信息量的数学期望=4× +5×
+5× +6×
+6× +7×
+7× +8×
+8× +9×
+9× =6.5
=6.5
分析:(1)由题意知通过的信息量ξ≥6,则可保证信息通畅.线路信息通畅包括四种情况,即通过的信息量分别为9,8,7,6,这四种情况是互斥的,根据互斥事件的概率公式和等可能事件的概率公式得到结果.
(2)ξ的所有可能取值为4,5,6,7,8,9,结合变量对应的事件和等可能事件的概率及互斥事件的概率,得到变量的概率,即可求出通过信息总量ξ的分布列和数学期望
点评:本题考查离散型随机变量的分布列与数学期望.概率、期望的计算是经常考查的内容,排列、组合知识是基础,掌握准确的分类和分步是解决概率问题的奠基石.属中档题.
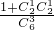 =
=
∵1+2+4=2+2+3=7,∴P(ξ=7)=
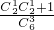 =
=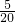 =
= ,
,∵2+2+4=1+3+4=8,∴P(ξ=8)=
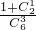 =
= ,
,∵2+3+4=9,∴P(ξ=9)=
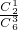 =
=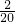 =
= ,
,∴线路信息畅通的概率是
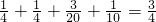 .
.(2)ξ=4,5,6,7,8,9
∵1+1+2=4,∴P(ξ=4)=
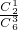 =
=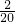 =
= ,
,∵1+1+3=1+2+2=5,∴P(ξ=5)=
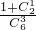 =
= ,
,ξ的分布列为
| ξ | 4 | 5 | 6 | 7 | 8 | 9 |
| P |  |  |  |  |  |  |
 +5×
+5× +6×
+6× +7×
+7× +8×
+8× +9×
+9× =6.5
=6.5分析:(1)由题意知通过的信息量ξ≥6,则可保证信息通畅.线路信息通畅包括四种情况,即通过的信息量分别为9,8,7,6,这四种情况是互斥的,根据互斥事件的概率公式和等可能事件的概率公式得到结果.
(2)ξ的所有可能取值为4,5,6,7,8,9,结合变量对应的事件和等可能事件的概率及互斥事件的概率,得到变量的概率,即可求出通过信息总量ξ的分布列和数学期望
点评:本题考查离散型随机变量的分布列与数学期望.概率、期望的计算是经常考查的内容,排列、组合知识是基础,掌握准确的分类和分步是解决概率问题的奠基石.属中档题.

练习册系列答案
相关题目
 (2004•黄冈模拟)如图,A、B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.从中任取三条网线且使每条网线通过最大的信息量.
(2004•黄冈模拟)如图,A、B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4.从中任取三条网线且使每条网线通过最大的信息量. (2012•广州二模)如图,A,B两点之间有4条网线连接,每条网线能通过的最大信息量分别为1,2,3,4.从中任取两条网线,则这两条网线通过的最大信息量之和为5的概率是
(2012•广州二模)如图,A,B两点之间有4条网线连接,每条网线能通过的最大信息量分别为1,2,3,4.从中任取两条网线,则这两条网线通过的最大信息量之和为5的概率是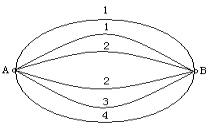 如图,A、B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中任取三条网线且使每条网线通过最大信息量.
如图,A、B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4,现从中任取三条网线且使每条网线通过最大信息量. (2012•广州二模)如图,A,B两点之间有6条网线连接,每条网线能通过的最大信息量分别为1,1,2,2,3,4.从中任取三条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息量之和为ξ.
(2012•广州二模)如图,A,B两点之间有6条网线连接,每条网线能通过的最大信息量分别为1,1,2,2,3,4.从中任取三条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息量之和为ξ.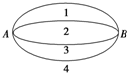 如图,A、B两点之间有4条网线连接,每条网线能通过的最大信息量分别为1,2,3,4.从中任取2条网线,则这2条网线通过的最大信息量之和等于5或6的概率是( )
如图,A、B两点之间有4条网线连接,每条网线能通过的最大信息量分别为1,2,3,4.从中任取2条网线,则这2条网线通过的最大信息量之和等于5或6的概率是( )