题目内容
若函数f(x)=
,g(x)=2|x+1|,则不等式f(x)>g(x)的解集是( )
|
分析:分别画出函数f(x)=
,g(x)=2|x+1|,的图象,如图.利用图象得到方程|x+1|2=2|x+1|(x>0)的两个根是1,3,再结合图象可得不等式f(x)>g(x)的解集.
|
解答: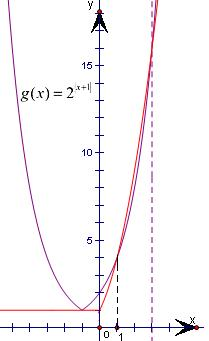 解:分别画出函数f(x)=
解:分别画出函数f(x)=
,g(x)=2|x+1|,的图象,如图.
方程|x+1|2=2|x+1|(x>0)的两个根是1,3,
结合图象可得不等式f(x)>g(x)的解集是(1,3).
故选C.
 解:分别画出函数f(x)=
解:分别画出函数f(x)=
|
方程|x+1|2=2|x+1|(x>0)的两个根是1,3,
结合图象可得不等式f(x)>g(x)的解集是(1,3).
故选C.
点评:本小题主要考查根的存在性及根的个数判断、分段函数的解析式求法及其图象的作法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目