题目内容
2.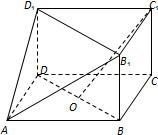 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.设O是线段BD的中点.
(1)求证:C1O∥平面AB1D1;
(2)证明:平面AB1D1⊥平面ADD1;
(3)求点D到平面ABD1的距离.
分析 (1)取B1D1的中点E,连接C1E,OA,易证C1EAO为平行四边形,从而得而C1O∥EA,利用线面平行的判定定理即可;
(2)可根据∠ABC=120°,AB=2,AD=4,证得∠ABD=$\frac{π}{2}$,即BD⊥AD,进一步可证BD⊥DD1,从而证得BD⊥平面ADD1,BD∥B1D1,于是得B1D1⊥平面ADD1,利用面面垂直的判定定理可得结论;
(3)利用等体积法,求点D到平面ABD1的距离.
解答 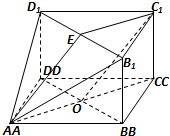 (1)证明:取B1D1的中点E,连接C1E,OA,则A,O,C共线,且C1E=OA,
(1)证明:取B1D1的中点E,连接C1E,OA,则A,O,C共线,且C1E=OA,
∵BCD-B1C1D1为三棱柱,
∴平面BCD∥平面B1C1D1,
故C1E∥OA,
∴C1EAO为平行四边形,
从而C1O∥EA,
又∵C1O?平面AB1D1,EA?平面AB1D1,
∴C1O∥平面AB1D1.
(2)证明:∵∠ABC=120°,AB=2,AD=4,
∴BD=$\sqrt{4+16-2×2×4×cos60°}$=2$\sqrt{3}$,
∴AD2=16=AD2+BD2,∠ABD=$\frac{π}{2}$,
即BD⊥AD,
又BB1⊥平面BCD,BD?平面BCD,BB1⊥BD,
在三棱柱BCD-B1C1D1中,BB1∥DD1,则BD⊥DD1,
而DD1∩AD=D,
∴BD⊥平面ADD1,
又BD∥B1D1,得B1D1⊥平面ADD1,
而B1D1?平面AB1D1,
∴平面AB1D1⊥平面ADD1;
(3)解:由题意,△AD1B中,AD1=$\sqrt{17}$,AB=2,BD1=$\sqrt{13}$,
∴$B{{D}_{1}}^{2}+A{B}^{2}=A{{D}_{1}}^{2}$,
∴${S}_{△AB{D}_{1}}$=$\frac{1}{2}×2×\sqrt{13}$=$\sqrt{13}$,
设点D到平面ABD1的距离为h,则
$\frac{1}{3}×\sqrt{13}h$=$\frac{1}{3}×\frac{1}{2}×4×2×sin60°×1$,
∴h=$\frac{2\sqrt{39}}{13}$.
点评 本题考查平面与平面垂直的判定与直线与平面平行的判定,考查点D到平面ABD1的距离,着重考查面面垂直与线面平行的判定定理的应用,注意使用定理的严谨性,属于中档题.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案