题目内容
13.已知f(x)=axekx-1,g(x)=lnx+kx.(Ⅰ)当a=1时,若f(x)在(1,+∞)上为减函数,g(x)在(0,1)上为增函数,求k的值;
(Ⅱ)对于任意k>0,f(x)≥g(x)恒成立,求实数a的取值范围.
分析 (I)利用导数与函数的单调性的关系可得:由于f(x)在(1,+∞)上为减函数,f′(x)≤0,在(1,+∞)上恒成立;由g(x)在(0,1)上为增函数,g′(x)≥0在在(0,1)上恒成立,解出k即可.
(II)设h(x)=f(x)-g(x)=axekx-lnx-kx-1(x>0),h′(x)=a(1+kx)ekx-$\frac{1}{x}$-k=(kx+1)$(a{e}^{kx}-\frac{1}{x})$.设u(x)=$a{e}^{kx}-\frac{1}{x}$.再利用导数研究其单调性,进而得到u(x)的零点,即可得出h(x)的极小值即最小值.
解答 解:(I)当a=1时,f(x)=xekx-1,∴f′(x)=ekx(1+kx),
∵f(x)在(1,+∞)上为减函数,
∴f′(x)≤0,在(1,+∞)上恒成立,
∴ekx(1+kx)≤0,解得k≤-$\frac{1}{x}$.
∵x>1,∴$\frac{-1}{x}$>-1,
∴k≤-1.
由g(x)=lnx+kx,可得${g}^{′}(x)=\frac{1}{x}+k$.
∵g(x)在(0,1)上为增函数,
∴${g}^{′}(x)=\frac{1}{x}+k$≥0在在(0,1)上恒成立,
即k$≥-\frac{1}{x}$,∵$\frac{1}{x}>1$,∴k≥-1.
综上可得:k=-1.
(II)设h(x)=f(x)-g(x)=axekx-lnx-kx-1(x>0),h′(x)=a(1+kx)ekx-$\frac{1}{x}$-k,
∴h′(x)=(kx+1)$(a{e}^{kx}-\frac{1}{x})$.
设u(x)=$a{e}^{kx}-\frac{1}{x}$.
①当a≤0时,u(x)<0,h(x)在(0,+∞)上单调递减,h(x)>0不恒成立;
②当a>0时,u′(x)=$ak{e}^{kx}+\frac{1}{{x}^{2}}$>0,则u(x)在(0,+∞)上为增函数.
u(x)的函数值由负到正,必有x0∈(0,+∞),使u(x0)=0.即$a{e}^{k{x}_{0}}$=$\frac{1}{{x}_{0}}$,两边取对数得:lna+kx0=-lnx0.
h(x)在(0,x0)上为减函数,在(x0,+∞)上为增函数.
h(x)min=h(x0)=ax0ekx0-1-lnx0-kx0=1-1-lnx0-kx0=lna.
∴lna≥0,即a∈[1,+∞).
点评 本题考查了利用导数研究函数的单调性极值与最值,考查了函数零点存在但是无法求出的情况下研究函数的单调性极值问题,考查了分类讨论思想方法,考查了推理能力与计算能力,属于难题.

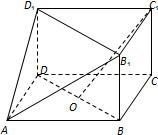 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.