题目内容
已知![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,
![]() ,
, ![]() .
.
(I)求证:数列![]() 是等比数列;
是等比数列;
(II)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(I)证明见答案(II)![]()
解析:
(I)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
即![]() .
.
又若an≠1,则an+1≠1,事实上当an≠1时,由![]() 知
知![]() ,若an+1=1,则an=1,从而与an≠1矛盾,故an+1≠1.
,若an+1=1,则an=1,从而与an≠1矛盾,故an+1≠1.
由此及![]() ≠1可知an≠1对任意n∈N
≠1可知an≠1对任意n∈N![]() 都成立.
都成立.
故对任何![]() ,
,![]() ,
,
所以![]() .
.
∵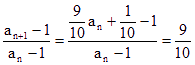 ,
,
∴![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(II)由![]() ,得
,得![]()
依题意(*)式对任意![]() 恒成立,
恒成立,
①当t=0时,(*)式显然不成立,因此t=0不符合题意.
②当t<0时,由![]()
![]() ,可知
,可知![]() (
(![]() ).
).
而当m是偶数时![]() ,因此t<0不符合题意.
,因此t<0不符合题意.
③当t>0时,由![]() (
(![]() ),
),
∴![]() ,∴
,∴![]() .(
.(![]() )
)
设![]() (
(![]() ),
),
∵![]() =
=![]() ,
,
∴![]() .
.
∴![]() 的最大值为
的最大值为![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
 ,数列
,数列 满足
满足 。
。 ;
; ,数列
,数列 满足
满足 ,
, ;数列
;数列 的前
的前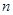 项和为
项和为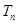 ,数列
,数列 ,
,
 .
. ;
;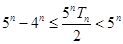 .
.  ,数列
,数列 满足
满足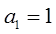 ,
,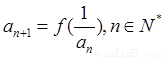 .
. 的通项公式;
的通项公式; 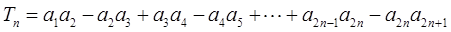 ,求
,求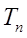 ;
; ,
, ,
, ,若
,若 对一切
对一切 成立,求最小正整数
成立,求最小正整数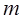 .
.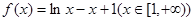 ,数列
,数列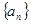 满足
满足 .
. ;
; ;
;