题目内容
(本题满分14分)已知函数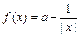 .
.
(1)判断函数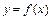 在
在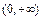 上的单调性,不用证明;
上的单调性,不用证明;
(2)若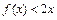 在
在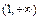 上恒成立,求实数
上恒成立,求实数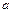 的取值范围;
的取值范围;
(3)若函数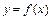 在
在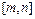 上的值域是
上的值域是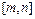
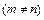 ,求实数
,求实数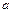 的取值范围.
的取值范围.
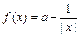 .
.(1)判断函数
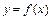 在
在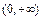 上的单调性,不用证明;
上的单调性,不用证明;(2)若
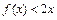 在
在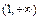 上恒成立,求实数
上恒成立,求实数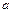 的取值范围;
的取值范围;(3)若函数
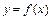 在
在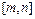 上的值域是
上的值域是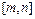
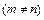 ,求实数
,求实数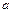 的取值范围.
的取值范围.(1) ,
, ,为增函数.
,为增函数.
(2)
(3)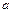 的取值范围是
的取值范围是 或
或 .
.
 ,
, ,为增函数.
,为增函数.(2)

(3)
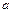 的取值范围是
的取值范围是 或
或 .
.(1) ,
, ,为增函数.……………………………………(3分)
,为增函数.……………………………………(3分)
(2)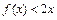 在
在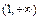 上恒成立,即
上恒成立,即 ,即
,即 在
在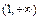 上恒成立.
上恒成立.
 小于
小于 ,
, 的最小值.
的最小值.
又 上为增函数
上为增函数

 …………………………………………………………(7分)
…………………………………………………………(7分)
(3)若 ,由(1)可知,
,由(1)可知,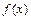 在
在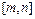 上有增函数.
上有增函数.
 即
即
 、
、 是方程
是方程 的两不同实根,
的两不同实根, ,
, .…………(10分)
.…………(10分)
若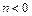 时,
时, 在
在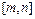 上有为减函数.
上有为减函数.
 ,
, ,
, ,
, . …………(13分)
. …………(13分)
故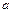 的取值范围是
的取值范围是 或
或 .………………………………………………………(14分)
.………………………………………………………(14分)
 ,
, ,为增函数.……………………………………(3分)
,为增函数.……………………………………(3分)(2)
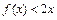 在
在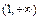 上恒成立,即
上恒成立,即 ,即
,即 在
在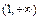 上恒成立.
上恒成立. 小于
小于 ,
, 的最小值.
的最小值.又
 上为增函数
上为增函数
 …………………………………………………………(7分)
…………………………………………………………(7分)(3)若
 ,由(1)可知,
,由(1)可知,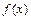 在
在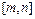 上有增函数.
上有增函数. 即
即
 、
、 是方程
是方程 的两不同实根,
的两不同实根, ,
, .…………(10分)
.…………(10分)若
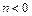 时,
时, 在
在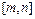 上有为减函数.
上有为减函数. ,
, ,
, ,
, . …………(13分)
. …………(13分)故
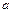 的取值范围是
的取值范围是 或
或 .………………………………………………………(14分)
.………………………………………………………(14分)
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
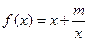 ,且此函数图像过点(1,5).
,且此函数图像过点(1,5).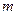 的值;
的值;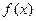 奇偶性;
奇偶性;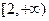 上的单调性,并用定义证明你的结论.
上的单调性,并用定义证明你的结论.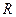 上的增函数
上的增函数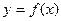 对任意
对任意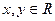 都有
都有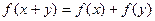 。
。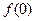 ;
;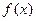 为奇函数;
为奇函数;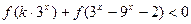 对任意
对任意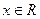 恒成立,求实数
恒成立,求实数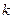 的取值范围。
的取值范围。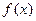 ,对任意
,对任意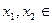 R,恒有:
R,恒有: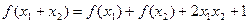 ,求:
,求: 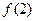 的值;
的值;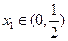 ,
,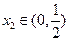 ,都有
,都有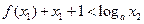 成立,求实数
成立,求实数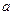 的取值范围.
的取值范围. 分别由下表给出
分别由下表给出


 ,当
,当 时,
时,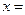 。
。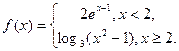 ,则
,则 的值为 ( )
的值为 ( ) 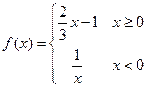 ,若
,若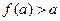 ,则实数a的取值范围是 ( )
,则实数a的取值范围是 ( )


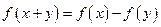 对于任意实数
对于任意实数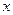 都成立,在区间
都成立,在区间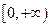 单调递增,则满足
单调递增,则满足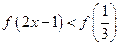 的
的
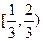



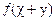 =
=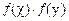 ,且
,且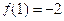 ,则
,则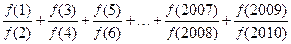 等于 ( ) A.—502.5 B.—1004 C.502.5 D.1004
等于 ( ) A.—502.5 B.—1004 C.502.5 D.1004