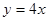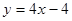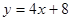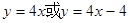题目内容
已知函数 .
.
(Ⅰ)若曲线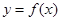 在点
在点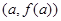 处与直线
处与直线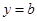 相切,求
相切,求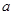 与
与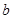 的值.
的值.
(Ⅱ)若曲线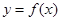 与直线
与直线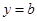 有两个不同的交点,求
有两个不同的交点,求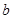 的取值范围.
的取值范围.
 .
.(Ⅰ)若曲线
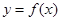 在点
在点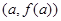 处与直线
处与直线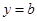 相切,求
相切,求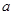 与
与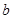 的值.
的值.(Ⅱ)若曲线
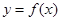 与直线
与直线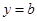 有两个不同的交点,求
有两个不同的交点,求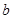 的取值范围.
的取值范围.(Ⅰ)求两个参数,需要建立两个方程。切点在切线上建立一个,利用导数的几何意义建立另一个,联立求解。(Ⅱ)利用导数分析曲线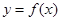 的走势,数形结合求解。
的走势,数形结合求解。
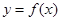 的走势,数形结合求解。
的走势,数形结合求解。因为 ,所以
,所以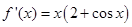 .
.
(Ⅰ)因为曲线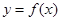 在点
在点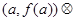 处与直线
处与直线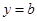 相切,
相切,
所以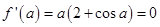 ,
,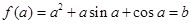 ,
,
解得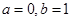 .
.
(Ⅱ)由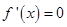 ,得
,得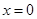 .
.
 和
和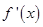 的情况如下:
的情况如下:
所以函数 在区间
在区间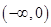 上单调递减,在区间
上单调递减,在区间 单调递增,
单调递增,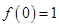 是函数的最小值.
是函数的最小值.
当 时,曲线
时,曲线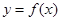 与直线
与直线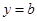 最多只有一个交点.
最多只有一个交点.
当 时,
时, ,
,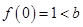 ,
,
所以,存在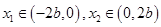 ,使得
,使得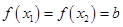 .
.
由于函数 在区间
在区间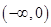 和
和 均单调,所以
均单调,所以 时,曲线
时,曲线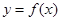 与直线
与直线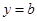 有且仅有两个交点.
有且仅有两个交点.
【考点定位】本题考查导数的计算、切线方程、导数的应用,故考查了运算求解能力.讨论直线和曲线的交点个数,故考查了分类讨论思想的应用.
 ,所以
,所以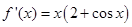 .
.(Ⅰ)因为曲线
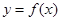 在点
在点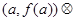 处与直线
处与直线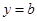 相切,
相切,所以
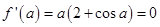 ,
,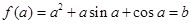 ,
,解得
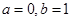 .
.(Ⅱ)由
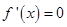 ,得
,得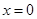 .
. 和
和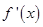 的情况如下:
的情况如下: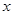 | 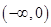 | 0 |  |
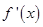 | - | 0 | + |
 |  | 1 |  |
 在区间
在区间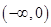 上单调递减,在区间
上单调递减,在区间 单调递增,
单调递增,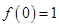 是函数的最小值.
是函数的最小值.当
 时,曲线
时,曲线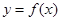 与直线
与直线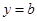 最多只有一个交点.
最多只有一个交点.当
 时,
时, ,
,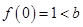 ,
,所以,存在
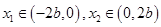 ,使得
,使得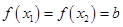 .
.由于函数
 在区间
在区间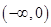 和
和 均单调,所以
均单调,所以 时,曲线
时,曲线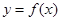 与直线
与直线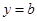 有且仅有两个交点.
有且仅有两个交点.【考点定位】本题考查导数的计算、切线方程、导数的应用,故考查了运算求解能力.讨论直线和曲线的交点个数,故考查了分类讨论思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;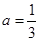 时,求函数
时,求函数 ,若对于
,若对于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求实数
成立,求实数 的取值范围.
的取值范围. 的图像在点
的图像在点 处的切线斜率为
处的切线斜率为 ,则
,则 的值是 .
的值是 .
 的单调区间;
的单调区间; 在
在 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; ,使
,使 成立,求实数
成立,求实数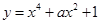 在点
在点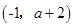 处切线的斜率为8,
处切线的斜率为8,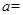 ( )
( )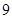
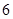
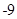
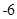
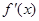 是函数f(x)的导函数,如果
是函数f(x)的导函数,如果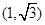
 ,那么曲线f(x)上任一点处的切线的倾斜角
,那么曲线f(x)上任一点处的切线的倾斜角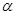 的取值范围是
的取值范围是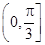
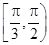
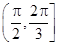
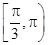
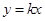 是
是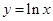 的切线,则
的切线,则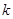 的值是 .
的值是 .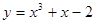 在P点处的切线平行于直线
在P点处的切线平行于直线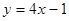 ,则此切线方程是( )
,则此切线方程是( )