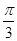题目内容
如图,已知抛物线的方程为x2=2px(p>0,为常数),过点M(0,m)且倾斜角为 的直线交抛物线于A(x1,y1),B(x2,y2)两点,且
的直线交抛物线于A(x1,y1),B(x2,y2)两点,且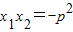
(1)求m的值
(2)若点M分AB所成的比为
 ,求直线AB的方程.
,求直线AB的方程.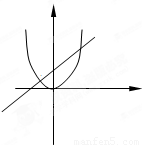
【答案】分析:(1)设AB方程为y=kx+m,代入x2=2py,得x2-2pkx-2pm=0,由此能求出m.
(2)设|AA1|=|AM|=t,则|BB1|=|BM|=2t,由此得到tanθ=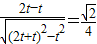 ,从而能求出AB的方程.
,从而能求出AB的方程.
解答:解:(1)设AB方程为y=kx+m代入x2=2py得x2-2pkx-2pm=0,①(3分)
由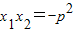 得,-2pm=-p2
得,-2pm=-p2
∴2m=p,即m=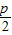 ,(6分)
,(6分)
(2)设|AA1|=|AM|=t,则|BB1|=|BM|=2t,
∴tanθ=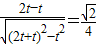 ,(10分)
,(10分)
故AB方程为y=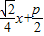 .(12分)
.(12分)
点评:本题考查直线方程的求法,解题时要认真审题,注意抛物线性质和等价转化思想的合理运用.
(2)设|AA1|=|AM|=t,则|BB1|=|BM|=2t,由此得到tanθ=
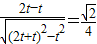 ,从而能求出AB的方程.
,从而能求出AB的方程.解答:解:(1)设AB方程为y=kx+m代入x2=2py得x2-2pkx-2pm=0,①(3分)
由
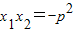 得,-2pm=-p2
得,-2pm=-p2∴2m=p,即m=
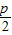 ,(6分)
,(6分)(2)设|AA1|=|AM|=t,则|BB1|=|BM|=2t,
∴tanθ=
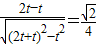 ,(10分)
,(10分)故AB方程为y=
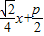 .(12分)
.(12分)点评:本题考查直线方程的求法,解题时要认真审题,注意抛物线性质和等价转化思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
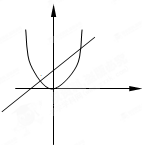 如图,已知抛物线的方程为x2=2px(p>0,为常数),过点M(0,m)且倾斜角为
如图,已知抛物线的方程为x2=2px(p>0,为常数),过点M(0,m)且倾斜角为 (2013•浙江模拟)如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于( )
(2013•浙江模拟)如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,设QB,BP与x轴分别相交于M,N两点.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN的大小等于( ) .(2007湖南示范) 如图,已知抛物线的方程为
.(2007湖南示范) 如图,已知抛物线的方程为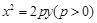 ,过点
,过点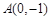 作直线
作直线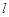 与抛物线相交于
与抛物线相交于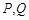 两点,点
两点,点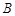 的坐标为
的坐标为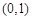 ,连接
,连接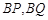 ,设
,设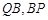 与
与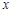 轴分别相交于
轴分别相交于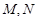 两点.如果
两点.如果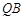 的斜率与
的斜率与 的斜率的乘积为
的斜率的乘积为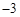 ,则
,则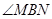 的大小等于( )
的大小等于( )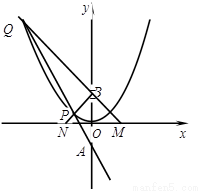
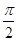 B.
B.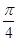 C.
C.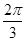 D.
D.