题目内容
直线l:y=2x是三角形中∠C的平分线所在直线,若点A(-4,2),B(3,1).
(1)求点A关于直线l(2)的对称点D的坐标;
(3)求点C的坐标;
(4)求三角形ABC的高CE所在的直线方程.
(1)求点A关于直线l(2)的对称点D的坐标;
(3)求点C的坐标;
(4)求三角形ABC的高CE所在的直线方程.
分析:(1)设出对称点D的坐标,利用垂直与平分列出方程组,求出D的坐标;
(3)求出BC的方程,通过C的平分线方程,求解方程组,即可求点C的坐标;
(4)利用点斜式方程,直接求三角形ABC的高CE所在的直线方程.
(3)求出BC的方程,通过C的平分线方程,求解方程组,即可求点C的坐标;
(4)利用点斜式方程,直接求三角形ABC的高CE所在的直线方程.
解答:解:(1)设D(m,n)
⇒
∴D(4,-2)
(2)∵D点在直线BC上,∴直线BC的方程为3x+y-10=0
又因为C在直线y=2x上,所以
⇒
所以C(2,4).
(3)三角形ABC的高CE,∵kAB=
=-
,
∴kCE=7,C(2,4).
所以直线CE的方程为y-4=7(x-2),
所求直线方程为:7x-y-10=0.
|
|
(2)∵D点在直线BC上,∴直线BC的方程为3x+y-10=0
又因为C在直线y=2x上,所以
|
|
(3)三角形ABC的高CE,∵kAB=
| 2-1 |
| -4-3 |
| 1 |
| 7 |
∴kCE=7,C(2,4).
所以直线CE的方程为y-4=7(x-2),
所求直线方程为:7x-y-10=0.
点评:本题考查点关于直线的对称点,直线方程的求法,考查计算能力.

练习册系列答案
相关题目
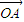 ,
,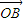 ,
,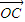 满足
满足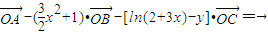 ,记y=f(x).
,记y=f(x).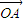 、
、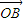 、
、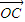 满足
满足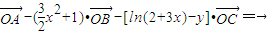 ,记y=f(x).
,记y=f(x).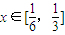 ,
,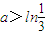 ,证明:不等式|a-lnx|>ln[f′(x)-3x]成立;
,证明:不等式|a-lnx|>ln[f′(x)-3x]成立;