题目内容
若关于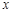 的不等式
的不等式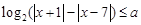 恒成立,则
恒成立,则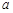 的取值范围是( )
的取值范围是( )
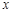 的不等式
的不等式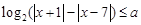 恒成立,则
恒成立,则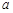 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
A
析:由题意知不等式的解集是R,可转化为求函数的最大值,利用绝对值的几何意义(到-1、7的距离之差最大值是8)不难得到答案.
解答:解:∵关于x的不等式log2(|x+1|-|x-7)≤a恒成立,
∴不等式log2(|x+1|-|x-7|)≤a的解集为R,
则a不小于log2(|x+1|-|x-7)的最大值,由绝对值的几何意义
知(|x+1|-|x-7|)的最大值:8
所以log2(|x+1|-|x-7|)的最大值是log28=3,
∴a≥3.
故选A.
点评:本题考查绝对值的几何意义,恒成立问题,考查转化思想的应用,是中档题.
解答:解:∵关于x的不等式log2(|x+1|-|x-7)≤a恒成立,
∴不等式log2(|x+1|-|x-7|)≤a的解集为R,
则a不小于log2(|x+1|-|x-7)的最大值,由绝对值的几何意义
知(|x+1|-|x-7|)的最大值:8
所以log2(|x+1|-|x-7|)的最大值是log28=3,
∴a≥3.
故选A.
点评:本题考查绝对值的几何意义,恒成立问题,考查转化思想的应用,是中档题.

练习册系列答案
相关题目
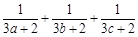 的最小值.
的最小值.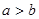 ,
,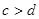 ,那么( )
,那么( )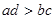

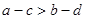
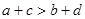
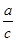 >
>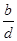
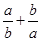 ≥2
≥2
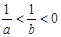 ,有下面四个不等式:(1)
,有下面四个不等式:(1)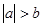 ;(2)a<b (3)a+b<ab; (4)
;(2)a<b (3)a+b<ab; (4) ,不正确的不等式的个数是( )
,不正确的不等式的个数是( )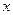 满足不等式
满足不等式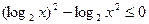 ,
, (
(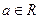 )的最小
)的最小 值.
值.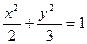 ,则
,则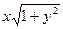 的最大值为
的最大值为 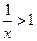 的解集是
的解集是