题目内容
(本题12分)已知椭圆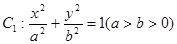 的左、右焦点分别为F1、F2,其中F2也是抛物线
的左、右焦点分别为F1、F2,其中F2也是抛物线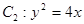 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
(I)求椭圆C1的方程; (II)已知菱形ABCD的顶点A、C在椭圆C1上,顶点B、D在直线 上,求直线AC的方程。
上,求直线AC的方程。
(I)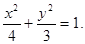 (II)直线AC的方程为
(II)直线AC的方程为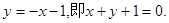
解析试题分析:(I)设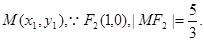 由抛物线定义,
由抛物线定义,
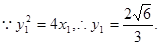 ,
, 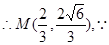 M点C1上,
M点C1上,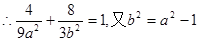
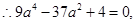
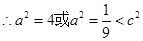 舍去.
舍去.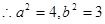
 椭圆C1的方程为
椭圆C1的方程为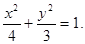
(II) 为菱形,
为菱形, ,设直线AC的方程为
,设直线AC的方程为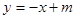
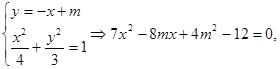
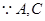 在椭圆C1上,
在椭圆C1上,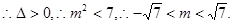 设
设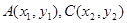 ,则
,则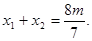

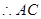 的中点坐标为
的中点坐标为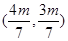 ,由ABCD为菱形可知,点
,由ABCD为菱形可知,点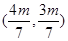 在直线BD:
在直线BD: 上,
上,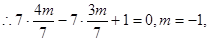
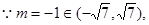 ∴直线AC的方程为
∴直线AC的方程为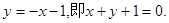
考点:本题主要考查抛物线的定义,椭圆标准方程及几何性质,直线与椭圆的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆标准方程时,主要运用了抛物线的定义及椭圆的几何性质。为求直线AC的方程,本题利利用了待定系数法,通过联立方程组,应用韦达定理,确定了AC、BD的中点坐标,代人已知方程,得到“待定系数”,达到了解题目的。

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 轴,且实轴长为2,离心率
轴,且实轴长为2,离心率 , L是过定点
, L是过定点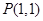 的直线.
的直线.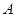 ,
,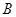 两点,且线段
两点,且线段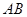 恰好以点
恰好以点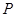 为中点,若存在,求出直线L的方程,若不存,说明理由.
为中点,若存在,求出直线L的方程,若不存,说明理由.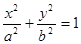 (
(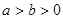 )过点
)过点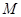 (0,2),离心率
(0,2),离心率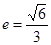 .
.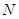 (2,0)的直线
(2,0)的直线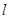 与椭圆相交于
与椭圆相交于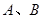 两点,且
两点,且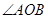 为锐角(其中
为锐角(其中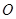 为坐标原点),求直线
为坐标原点),求直线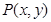 到直线
到直线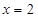 的距离与它到定点
的距离与它到定点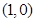 的距离之比为
的距离之比为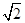 ,并记点
,并记点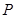 的轨迹为曲线
的轨迹为曲线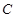 .
.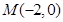 ,过点
,过点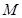 的直线
的直线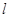 与曲线
与曲线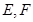 两点,当线段
两点,当线段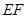 的中点落在由四点
的中点落在由四点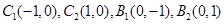 构成的四边形内(包括边界)时,求直线
构成的四边形内(包括边界)时,求直线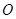 为极点,
为极点,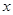 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线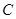 的极坐标方程是
的极坐标方程是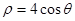 ,直线
,直线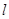 的参数方程是
的参数方程是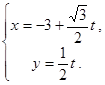 (
( 为参数)。
为参数)。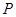 的极坐标;
的极坐标; 、
、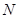 分别为曲线
分别为曲线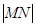 的最小值。
的最小值。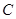 :
: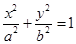 (
(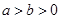 )的离心率为
)的离心率为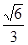 ,过右焦点
,过右焦点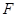 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆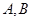 两点,
两点,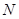 为弦
为弦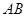 的中点。
的中点。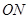 (
( 为坐标原点)的斜率
为坐标原点)的斜率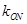 ;
;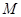 椭圆
椭圆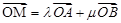 ,求
,求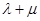 的最大值和最小值.
的最大值和最小值.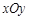 中,点
中,点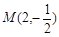 ,点
,点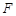 为抛物线
为抛物线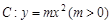 的焦点,
的焦点,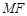 恰被抛物线
恰被抛物线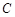 平分.
平分.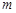 的值;
的值;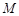 作直线
作直线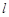 交抛物线
交抛物线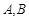 两点,设直线
两点,设直线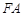 、
、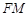 、
、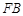 的斜率分别为
的斜率分别为 、
、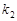 、
、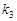 ,问
,问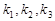 能否成公差不为零的等差数列?若能,求直线
能否成公差不为零的等差数列?若能,求直线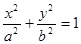 (
(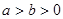 )过点
)过点 (0,2),离心率
(0,2),离心率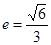 .
.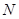 (2,0)的直线
(2,0)的直线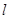 与椭圆相交于
与椭圆相交于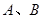 两点,且
两点,且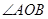 为锐角(其中
为锐角(其中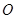 为坐标原点),求直线
为坐标原点),求直线 与直线
与直线 相交于
相交于 两点,且
两点,且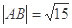
 的值。
的值。 上是否存在点
上是否存在点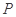 ,使得
,使得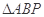 的重心恰为抛物线
的重心恰为抛物线 ,若存在,求点
,若存在,求点