题目内容
将五名志愿者随机地分到A,B,C三个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求恰有两名志愿者参加A岗位服务的概率;
(2)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列.
解:将五名志愿者随机地分到A,B,C三个不同的岗位服务的基本事件总数为(C52•C32/A22+C53)•A33=150.
(1)记恰有两名志愿者参加A岗位服务为事件EA,则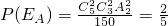 ,即恰有两名志愿者参加A岗位服务的概率是
,即恰有两名志愿者参加A岗位服务的概率是 .
.
(2)由题意知随机变量ξ可能取的值为1,2,3,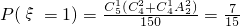 ;
;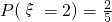 ,
, ,所以ξ的分布列是
,所以ξ的分布列是
分析:(1)先恰有两名志愿者参加A岗位服务的方法总数及将五名志愿者随机地分到A,B,C三个不同的岗位服务的基本事件总数,最后利用概率公式计算即可.
(2)五名志愿者中参加A岗位服务的人数ξ可能的取值是1、2、3,“ξ=2”是指有两人同时参加A岗位服务,同第一问类似做出结果.最后写出分布列.
点评:本题考查概率,随机变量的分布列,近几年新增的内容,整体难度不大,可以作为高考基本得分点.总的可能性是典型的“捆绑排列”,易把C53混淆为A53.
(1)记恰有两名志愿者参加A岗位服务为事件EA,则
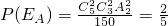 ,即恰有两名志愿者参加A岗位服务的概率是
,即恰有两名志愿者参加A岗位服务的概率是 .
.(2)由题意知随机变量ξ可能取的值为1,2,3,
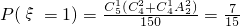 ;
;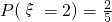 ,
, ,所以ξ的分布列是
,所以ξ的分布列是| ξ | 1 | 2 | 3 |
| P | 7/15 | 2/5 | 2/15 |
分析:(1)先恰有两名志愿者参加A岗位服务的方法总数及将五名志愿者随机地分到A,B,C三个不同的岗位服务的基本事件总数,最后利用概率公式计算即可.
(2)五名志愿者中参加A岗位服务的人数ξ可能的取值是1、2、3,“ξ=2”是指有两人同时参加A岗位服务,同第一问类似做出结果.最后写出分布列.
点评:本题考查概率,随机变量的分布列,近几年新增的内容,整体难度不大,可以作为高考基本得分点.总的可能性是典型的“捆绑排列”,易把C53混淆为A53.

练习册系列答案
相关题目