题目内容
甲乙丙丁4人玩传球游戏,持球者将球等可能的传给其他3人,若球首先从甲传出,经过3次传球.
(1)求球恰好回到甲手中的概率;
(2)设乙获球(获得其他游戏者传的球)的次数为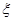 ,求
,求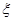 的分布列及数学期望.
的分布列及数学期望.
(1)求球恰好回到甲手中的概率;
(2)设乙获球(获得其他游戏者传的球)的次数为
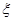 ,求
,求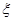 的分布列及数学期望.
的分布列及数学期望.(1)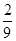 ;(2)分布列详见解析,
;(2)分布列详见解析,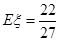 .
.
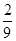 ;(2)分布列详见解析,
;(2)分布列详见解析,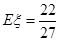 .
.试题分析:本题主要考查古典概型和离散型随机变量的分布列和数学期望等数学知识,考查学生的分析问题解决问题的能力和计算能力.第一问,利用古典概型先求出经过3次传球的传球方法共27种,再求3次传球后,求恰好回到甲手中的种数,相除得到概率值;第二问,先分别求出
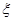 的3种情况的概率,概率的分子可以用树状图数出来,列出分布列,利用
的3种情况的概率,概率的分子可以用树状图数出来,列出分布列,利用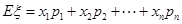 求出数学期望.
求出数学期望.试题解析:⑴
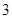 次传球,传球的方法共有
次传球,传球的方法共有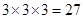 种,
种,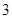 次传球结束时,球恰好回到甲手中的传球方法为
次传球结束时,球恰好回到甲手中的传球方法为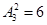 种,故所求概率为
种,故所求概率为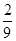 5分
5分⑵易知
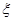 的所有可能取值为
的所有可能取值为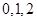 6分
6分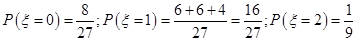 , 9分
, 9分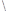
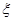 的分布列为
的分布列为 | 0 | 1 | 2 |
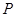 | 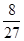 | 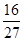 | 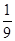 |
因此,
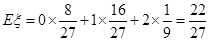 . 12分
. 12分
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 (如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为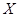 ,若
,若 就去打球,若
就去打球,若 就去唱歌,若
就去唱歌,若 就去下棋。
就去下棋。




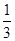 .那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________.
.那么这位司机遇到红灯前,已经通过了两个交通岗的概率是________. ,他连续测试两次,那么其中恰有一次通过的概率是( )
,他连续测试两次,那么其中恰有一次通过的概率是( )

