题目内容
函数f(x)=x|x+a|+b是奇函数的充要条件是( )
| A.ab="0" | B.a+b="0" | C.a=b | D. =0 =0 |
D
解析考点:函数奇偶性的判断;必要条件、充分条件与充要条件的判断.
专题:计算题.
分析:利用奇函数的定义“函数y=f(x)的定义域为D,如果对D内的任意一个x,都有x∈D,且f(-x)=-f(x),则这个函数叫做奇函数”建立恒等式,求出a、b的值即可.
解答:解:根据奇函数的定义可知
f(-x)=-x|a-x|+b=-f(x)=-x|x+a|-b对任意x恒成立
∴a=0,b=0,故选D
点评:本题主要考查了函数奇偶性的判断,以及必要条件、充分条件与充要条件的判断,属于基础题.

练习册系列答案
相关题目
函数 的图象与函数
的图象与函数 的图象关于直线对称,则
的图象关于直线对称,则
A.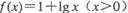 | B.t |
C. | D. |
已知实数 ,函数
,函数 上是减函数,函数
上是减函数,函数 ,则下列选项正确的是 ( )
,则下列选项正确的是 ( )
A. | B. |
C. | D. |
定义在 上的偶函数满足
上的偶函数满足 且
且 在
在 上为减函数,若
上为减函数,若 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则
 ( )
( )
A.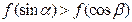 | B. |
C. | D. |
已知定义在 上的函数
上的函数 为奇函数,则
为奇函数,则 的值是( )
的值是( )
A. | B. | C. | D. |
下列结论正确的是 ( )
A.当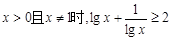 | B.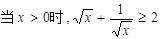 |
C.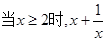 的最小值为2 的最小值为2 | D.当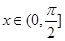 时, 时, 的最小值是4 的最小值是4 |
 是偶函数,当
是偶函数,当 >0 时,
>0 时, ,且当
,且当 时,
时, 成立,则
成立,则 的最小值为
的最小值为 B.
B. C.
C.  D. 1
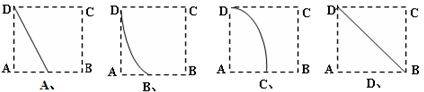
D. 1 为正三角形,四边形ABCD为正方形,平面
为正三角形,四边形ABCD为正方形,平面 .点M为平面ABCD内的一个动点,且满足
.点M为平面ABCD内的一个动点,且满足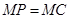 .则点M在正方形ABCD内的轨迹为
.则点M在正方形ABCD内的轨迹为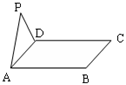
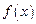 的反函数
的反函数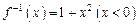 ,则
,则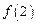
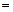 ( )
( )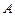 .1
.1 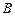 .
.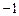
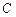 .1或
.1或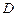 .5
.5