题目内容
在数列![]() 中,已知
中,已知![]() ,且
,且![]() .
.
(1)若数列![]() 为等差数列,求p的值;
为等差数列,求p的值;
(2)求数列![]() 的前n项和
的前n项和![]() ;
;
(3)当![]() 时,求证:
时,求证:![]() .
.
同下
解析:
(1)设数列{an}的公差为d,则an=a1+(n-1)d,an+1=a1+nd.
由题意得,[a1+(n-1)d](a1+nd)=n2+3n+2对n∈N*恒成立.
即d2n2+(2a1d-d2)n+(a12-a1d)=n2+3n+2.
所以即或
因为a1=p>0,故p的值为2. ……………………………………………………3分
(2)因为an+1×an=n2+3n+2=(n+1)(n+2),所以an+2×an+1=(n+2)(n+3).
所以=. ……………………………………………………………………5分
①当n为奇数,且n≥3时,=,=,…,=.
相乘得=,所以an=p.当n=1时也符合.
②当n为偶数,且n≥4时,=,=,…,=.
相乘得=,所以an=a2.
因为a1×a2=6,所以a2=.所以an=,当n=2时也符合.
所以数列{an}的通项公式为an= ………………………7分
当n为偶数时,Sn=p++2p++…+p+=p×+×
=p+.
当n为奇数时,Sn=p++2p++3p++…++p
=p×+×=p+.
所以Sn= ………………………10分
(3)当n为偶数时,ni=1=+++…++≥4(++…+)
=4[++…+]
>2[+++…++]
=2(-+-+…+-)=.…………13分
当n为奇数,且n≥2时, ni=1=+++…++
≥4(++…+)+>4(++…+)
>2(++…++)=.
…………………………………………………………15分
又因为对任意n∈N*,都有<,
故当n≥2时,ni=1>.…………………………………………………………16分

练习册系列答案
相关题目
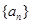 中,已知
中,已知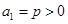 ,且
,且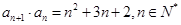 .
.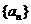 中,已知
中,已知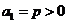 ,且
,且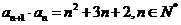 .
.