题目内容
 若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S.
若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S.(1)设z=2a-b,求z的取值范围;
(2)过点(-5,1)的一束光线,射到x轴被反射后经过区域S,求反射光线所在直线l经过区域S内的整点(即横纵坐标为整数的点)时直线l的方程.
【答案】分析:(1)令f(x)=x2+ax+b,根据题意可知f(0)>0,f(1)<0,f(3)>0,进而求得b>0,a+b+1<0,a+b+9>0,画出可行域,进而分别求得z的最大和最小值,答案可得.
(2)过点(-5,1)的光线经x轴反射后的光线必过点(-5,-1),由图可知,找出可能满足条件的整点,再结合不等式知点(-3,1)符合条件,得到此时直线方程即可.
解答: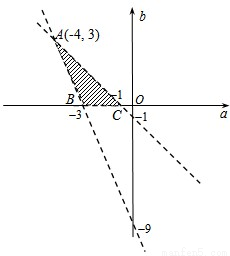 解:方程x2+ax+b=0的两根在区间(0,1)和(1,3)上的几何意义是:
解:方程x2+ax+b=0的两根在区间(0,1)和(1,3)上的几何意义是:
函数y=f(x)=x2+ax+b与x轴的两个交点的横坐标分别在区间(0,1)和(1,3)内,
由此可得不等式组
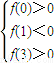 ,即
,即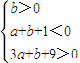 ,
,
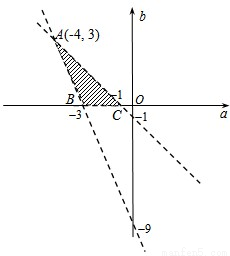
则在坐标平面aOb内,点(a,b)对应的区域S如图阴影部分所示,
易得图中A,B,C三点的坐标分别为(-4,3),(-3,0),(-1,0),(4分)
(1)令z=2a-b,则直线b=2a-z经过点A时z取到下边界-11,经过点C时z取到上边界-2,
又A,B,C三点的值没有取到,所以-11<z<-2;(8分)
(2)过点(-5,1)的光线经x轴反射后的光线必过点(-5,-1),由图可知
可能满足条件的整点为(-3,1),(-3,2),(-2,2),(-2,1),
再结合不等式知点(-3,1)符合条件,所以此时直线方程为:y+1=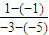 -(x+5),
-(x+5),
即y=x+4 (12分)
点评:本题主要考查了一元二次方程根据的分布,以及线性规划的基本知识.考查了学生对基础知识的综合运用.
(2)过点(-5,1)的光线经x轴反射后的光线必过点(-5,-1),由图可知,找出可能满足条件的整点,再结合不等式知点(-3,1)符合条件,得到此时直线方程即可.
解答:
 解:方程x2+ax+b=0的两根在区间(0,1)和(1,3)上的几何意义是:
解:方程x2+ax+b=0的两根在区间(0,1)和(1,3)上的几何意义是:函数y=f(x)=x2+ax+b与x轴的两个交点的横坐标分别在区间(0,1)和(1,3)内,
由此可得不等式组
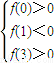 ,即
,即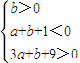 ,
,则在坐标平面aOb内,点(a,b)对应的区域S如图阴影部分所示,
易得图中A,B,C三点的坐标分别为(-4,3),(-3,0),(-1,0),(4分)
(1)令z=2a-b,则直线b=2a-z经过点A时z取到下边界-11,经过点C时z取到上边界-2,
又A,B,C三点的值没有取到,所以-11<z<-2;(8分)
(2)过点(-5,1)的光线经x轴反射后的光线必过点(-5,-1),由图可知
可能满足条件的整点为(-3,1),(-3,2),(-2,2),(-2,1),
再结合不等式知点(-3,1)符合条件,所以此时直线方程为:y+1=
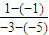 -(x+5),
-(x+5),即y=x+4 (12分)
点评:本题主要考查了一元二次方程根据的分布,以及线性规划的基本知识.考查了学生对基础知识的综合运用.

练习册系列答案
相关题目
 (2010•黄冈模拟)若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S.
(2010•黄冈模拟)若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S. 有两个根,一个根在区间
有两个根,一个根在区间 内,另一根在区间
内,另一根在区间 内,记点
内,记点 对应的区域为S。那么区域S的面积是_______.
对应的区域为S。那么区域S的面积是_______. 有两个根,一个根在区间
有两个根,一个根在区间 内,另一根在区间
内,另一根在区间 内,记点
内,记点 对应的区域为S。那么区域S的面积是_______.
对应的区域为S。那么区域S的面积是_______.