题目内容
已知顶点为原点 的抛物线
的抛物线 的焦点
的焦点 与椭圆
与椭圆 的右焦点重合
的右焦点重合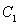 与
与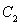 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为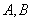 .
.
(1)若△AOB是边长为 的正三角形,求抛物线
的正三角形,求抛物线 的方程;
的方程;
(2)若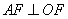 ,求椭圆
,求椭圆 的离心率
的离心率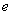 ;
;
(3)点 为椭圆
为椭圆 上的任一点,若直线
上的任一点,若直线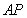 、
、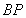 分别与
分别与 轴交于点
轴交于点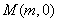 和
和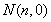 ,证明:
,证明: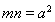 .
.
【答案】
(1) ;(2)
;(2)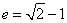 ;(3)证明过程详见试题解析.
;(3)证明过程详见试题解析.
【解析】
试题分析:(1)由△AOB是边长为 的正三角形得到
的正三角形得到 ,代入抛物线方程
,代入抛物线方程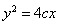 中,可以得到所求抛物线方程为
中,可以得到所求抛物线方程为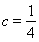 ;(2)由
;(2)由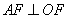 可知点
可知点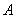 的横坐标是
的横坐标是 ,因此可结合
,因此可结合 建立关于
建立关于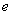 的方程为:
的方程为: ,解出
,解出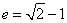 ;(3)利用设而不求的思想,可先设
;(3)利用设而不求的思想,可先设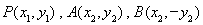 三点后代入椭圆方程中,由于
三点后代入椭圆方程中,由于 的方程为
的方程为 ,求出
,求出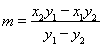 ,
,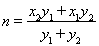 ,那么
,那么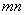 化简后得到:
化简后得到: .
.
试题解析:(1)设椭圆的右焦点为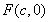 ,依题意得抛物线的方程为
,依题意得抛物线的方程为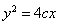
∵△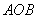 是边长为
是边长为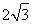 的正三角形,
的正三角形,
∴点A的坐标是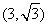 ,
,
代入抛物线的方程 解得
解得 ,
,
故所求抛物线 的方程为
的方程为
(2)∵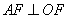 , ∴ 点
, ∴ 点 的横坐标是
的横坐标是
代入椭圆方程解得 ,即点
,即点 的坐标是
的坐标是
∵ 点 在抛物线
在抛物线 上,
上,
∴ ,
,
将 代入上式整理得:
代入上式整理得: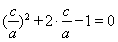 ,
,
即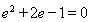 ,解得
,解得
∵  ,故所求椭圆
,故所求椭圆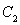 的离心率
的离心率 .
.
(3)证明:设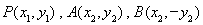 ,代入椭圆方程得
,代入椭圆方程得
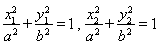
而直线 的方程为
的方程为
令 得
得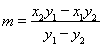 .
.
在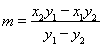 中,以
中,以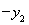 代换
代换 得
得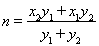
∴ 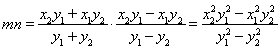
 .
.
考点:圆锥曲线;直线与圆锥曲线的位置关系.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆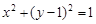 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求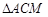 与
与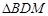 面积之和的最小值.
面积之和的最小值.
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0,  (p>0)的顶点关于直线l的对称点在该抛物的准线上.
(p>0)的顶点关于直线l的对称点在该抛物的准线上.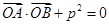 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.