题目内容
1.在△ABC中,角A,B,C所对的边分别为a,b,c,2(a2-b2)=2accosB+bc.(Ⅰ)求A;
(Ⅱ)D为边BC上一点,BD=3DC,∠DAB=$\frac{π}{2}$,求tanC.
分析 (Ⅰ)由余弦定理可得2accosB=a2+c2-b2,代入已知等式整理得cosA=-$\frac{1}{2}$,即可求得A.
(Ⅱ)由已知可求∠DAC=$\frac{π}{6}$,由正弦定理有$\frac{AD}{sinC}$=$\frac{CD}{sin∠DAC}$,又BD=3CD,可得3sinB=2sinC,由B=$\frac{π}{3}$-C化简即可得解.
解答 解:(Ⅰ)因为2accosB=a2+c2-b2,所以2(a2-b2)=a2+c2-b2+bc.…(2分)
整理得a2=b2+c2+bc,所以cosA=-$\frac{1}{2}$,即A=$\frac{2π}{3}$.…(4分)
(Ⅱ)因为∠DAB=$\frac{π}{2}$,所以AD=BD•sinB,∠DAC=$\frac{π}{6}$.…(6分)
在△ACD中,有$\frac{AD}{sinC}$=$\frac{CD}{sin∠DAC}$,又因为BD=3CD,
所以3sinB=2sinC,…(9分)
由B=$\frac{π}{3}$-C得$\frac{3\sqrt{3}}{2}$cosC-$\frac{3}{2}$sinC=2sinC,…(11分)
整理得tanC=$\frac{3\sqrt{3}}{7}$.…(12分)
点评 本题主要考查了余弦定理,正弦定理,同角三角函数关系式,三角函数恒等变换的应用,综合性较强,属于基本知识的考查.

练习册系列答案
相关题目
9.设Sn是数列{an}的前n项和,n∈*,若a1=1,Sn-1+Sn=3n2+2(n≥2)则S101的值为( )
| A. | 15601 | B. | 15599 | C. | 15449 | D. | 15451 |
16.函数y=4sin(ωx+φ)(ω>0,|φ|<π)部分图象如图,其中点A($\frac{2π}{3}$,0),B($\frac{8π}{3}$,0),则( )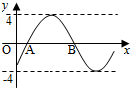

| A. | ω=$\frac{1}{2}$,φ=-$\frac{2π}{3}$ | B. | ω=1,φ=-$\frac{2π}{3}$ | C. | ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ | D. | ω=1,φ=-$\frac{π}{3}$ |
10.函数y=sin(2x+$\frac{3π}{4}$)的一条对称轴是( )
| A. | x=$\frac{π}{4}$ | B. | x=-$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=-$\frac{π}{8}$ |