题目内容
(文)已知:函数f(x)=  (a>1)
(a>1)
(1) 证明:函数f(x)在(-1,+∞ )上为增函数;
(2)证明方程f(x)=0没有负根.
【答案】
见解析。
【解析】(I)利用函数的单调性证明即可:第一步:取值,第二步作差比较,判断差值的符号,第三步得到结论.
(2)本小题不易直接证明可采用反证法,先假设方程有负根x0 (x0≠-1),则有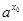 =
= -1,然后研究
-1,然后研究 -1的值总是负值,所以得到矛盾,问题得证.
-1的值总是负值,所以得到矛盾,问题得证.
(文)证明:(1) 设-1<x1<x2<+∞
f(x1)-f(x2)
= -
-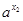 +
+
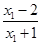 -
-
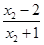
= -
-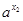 +
+
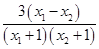 (4)
(4)
∵ -1<x1<x2 ,a>0
∴  -
-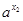 <0
<0
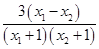 <0
<0
∴ f(x1)-f(x2)<0 即 f(x1)<f(x2) ,函数f(x)在(-1,+∞ )上为增函数. (6)
(2) 若方程有负根x0 (x0≠-1),则有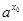 =
= -1
-1
若 x0<-1
,  -1<-1
而
-1<-1
而 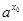 >0 故
>0 故 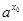 ≠
≠ -1
(10)
-1
(10)
若 -1<x0<0
,  -1>2
而
-1>2
而 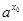 <a0=1
<a0=1 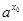 ≠
≠ -1
-1
综上所述,方程f(x)=0没有负根. (12)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (文)已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).
(文)已知函数f(x)=x3+ax2+bx+2与直线4x-y+5=0切于点P(-1,1).