题目内容

14．已知数列{bn}中，b1=4，且bn+1-2bn-4=0，则b8=（　　）
A．28-4B．210-4C．212-4D．29-4

分析 把已知数列递推式变形，可得{bn+4}构成以8为首项，以2为公比的等比数列．由此求出数列{bn}的通项公式得答案．

解答 解：由bn+1-2bn-4=0，得bn+1=2bn+4，
∴bn+1+4=2（bn+4），
又b1=4，∴b1+4=8≠0，
则$\frac{{b}_{n+1}+4}{{b}_{n}+4}$=2．
∴{bn+4}构成以8为首项，以2为公比的等比数列．
∴${b}_{n}+4=8•{2}^{n-1}={2}^{n+2}$．
∴${b}_{n}={2}^{n+2}-4$．
则b8=210-4．
故选：B．

点评 本题考查数列递推式，考查了等比关系的确定，是中档题．

练习册系列答案
相关题目
5．已知集合A={1，2，3，4}，B={3，4，5}，求A∩B，A∪B．
5．下列命题中，真命题的个数是（　　）
①?α，β∈R，使得cos（α+β）=cosα+cosβ；
②若函数f（x）=|log2（x+1）|，则?x1，x2∈（-1，1）且x1＜x2，使得f（x1）＞f（x2）；
③若$\overrightarrow{a}$，$\overrightarrow{b}$是两个非零向量，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|是$\overrightarrow{a}$⊥$\overrightarrow{b}$的充要条件；
④若ac2≥bc2则a≥b．
A．4B．3C．2D．1
2．设函数f（x）=ax2-bx+3，且f（x）＞0的解集为（-1，3），
（1）求函数f（x）的表达式；
（2）设g（x）=$\frac{f（x）}{x}$，若g（3+2sinθ）≥$\frac{1}{5}$m2-$\frac{12}{5}$m对任意θ∈R恒成立，则实数m的取值范围．
9．A，B两点在半径为2的球面上，且以线段AB为直径的小圆周长为2π，则A，B两点间的球面距离为（　　）
A．πB．2πC．$\frac{π}{3}$D．$\frac{2π}{3}$
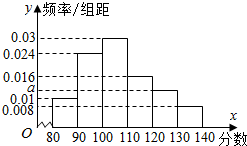19．某校在2015年11月份的高三期中考试后，随机地抽取了50名学生的数学成绩并进行了分析，结果这50名同学的成绩全部介于80分到140分之间．现将结果按如下方式分为6组，第一组[80，90），第二组[90，100），…，第六组[130，140]，得到如图所示的频率分布直方图．
（I）求a的值；
（II）这50名学生中成绩在120分以上的同学中任意抽取3人，该3人在130分（含130分）以上的人数记为X，求X的分布列和期望．
6．两个球的半径之比为1：3，那么这两个球的表面积之比为（　　）
A．1：9B．1：27C．1：3D．1：3$\sqrt{3}$
3．i•z=i-1（i为虚数单位），则z=（　　）
A．1-iB．-1+iC．1+iD．-1-i
4．已知：数列{an}的前n项和为Sn，满足Sn=2an-2n（n∈N*）
（1）证明数列{an+2}是等比数列．并求数列{an}的通项公式an；
（2）若数列{bn}满足bn=log2（an+2），而Tn为数列{$\frac{{b}_{n}}{{a}_{n}+2}$}的前n项和，求Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网