题目内容
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.(Ⅰ)求动圆圆心的轨迹M的方程;
(Ⅱ)设过点P,且斜率为-
 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
【答案】分析:(Ⅰ)利用条件直接代入抛物线的标准方程即可.
(Ⅱ)(i)先求出点A,B的坐标,再把点C设出来,利用△ABC为正三角形对应的|BC|=|AB|且|AC|=|AB|,看能否求出点C的坐标即可.
(ii)分三种情况分别求当△ABC为钝角三角形时,对应点C的纵坐标的取值范围即可.
解答:解:(Ⅰ)依题意,曲线M是以点P为焦点,
直线l为准线的抛物线,所以曲线M的方程为y2=4x.
(Ⅱ)(i)由题意得,
直线AB的方程为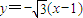 由
由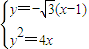
消y得3x2-10x+3=0,解得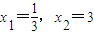 .
.
所以A点坐标为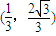 ,
,
B点坐标为(3, ),
),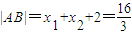 .
.
假设存在点C(-1,y),
使△ABC为正三角形,则|BC|=|AB|且|AC|=|AB|,
即①②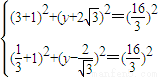
由①-②得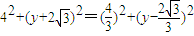 ,
,
解得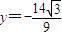 .
.
但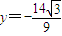 不符合①,
不符合①,
所以由①,②组成的方程组无解.
因此,直线l上不存在点C,
使得△ABC是正三角形.
(ii)设C(-1,y)使△ABC成钝角三角形,
由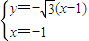 得
得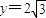 ,
,
即当点C的坐标为(-1,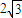 )时,A,B,C三点共线,
)时,A,B,C三点共线,
故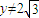 .
.
又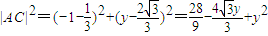 ,
,
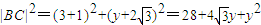 ,
,
 .
.
当|BC|2>|AC|2+|AB|2,
即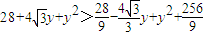 ,
,
即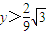 时,∠CAB为钝角.
时,∠CAB为钝角.
当|AC|2>|BC|2+|AB|2,
即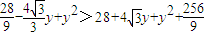 ,
,
即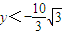 时∠CBA为钝角.
时∠CBA为钝角.
又|AB|2>|AC|2+|BC|2,
即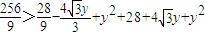 ,
,
即 .
.
该不等式无解,所以∠ACB不可能为钝角.
因此,当△ABC为钝角三角形时,
点C的纵坐标y的取值范围是 或
或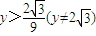 .
.
点评:本小题主要考查直线、圆与抛物线的基本概念及位置关系,考查运用解析几何的方法解决数学问题的能力.
(Ⅱ)(i)先求出点A,B的坐标,再把点C设出来,利用△ABC为正三角形对应的|BC|=|AB|且|AC|=|AB|,看能否求出点C的坐标即可.
(ii)分三种情况分别求当△ABC为钝角三角形时,对应点C的纵坐标的取值范围即可.
解答:解:(Ⅰ)依题意,曲线M是以点P为焦点,
直线l为准线的抛物线,所以曲线M的方程为y2=4x.
(Ⅱ)(i)由题意得,
直线AB的方程为
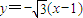 由
由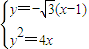
消y得3x2-10x+3=0,解得
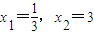 .
.所以A点坐标为
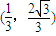 ,
,B点坐标为(3,
 ),
),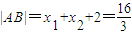 .
.假设存在点C(-1,y),
使△ABC为正三角形,则|BC|=|AB|且|AC|=|AB|,
即①②
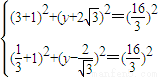
由①-②得
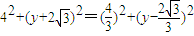 ,
,解得
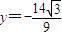 .
.但
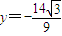 不符合①,
不符合①,所以由①,②组成的方程组无解.
因此,直线l上不存在点C,
使得△ABC是正三角形.
(ii)设C(-1,y)使△ABC成钝角三角形,
由
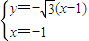 得
得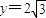 ,
,即当点C的坐标为(-1,
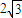 )时,A,B,C三点共线,
)时,A,B,C三点共线,故
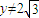 .
.又
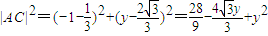 ,
,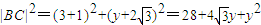 ,
, .
.当|BC|2>|AC|2+|AB|2,
即
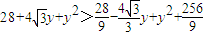 ,
,即
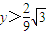 时,∠CAB为钝角.
时,∠CAB为钝角.当|AC|2>|BC|2+|AB|2,
即
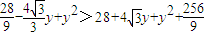 ,
,即
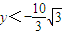 时∠CBA为钝角.
时∠CBA为钝角.又|AB|2>|AC|2+|BC|2,
即
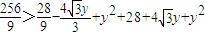 ,
,即
 .
.该不等式无解,所以∠ACB不可能为钝角.
因此,当△ABC为钝角三角形时,
点C的纵坐标y的取值范围是
 或
或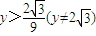 .
.点评:本小题主要考查直线、圆与抛物线的基本概念及位置关系,考查运用解析几何的方法解决数学问题的能力.

练习册系列答案
相关题目
 已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.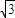 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.