题目内容
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-
的直线与曲线M相交于A、B两点.问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-
| 3 |
分析:(1)由动圆过定点P(1,0),且与定直线l:x=-1相切,结合抛物线的定义得动圆圆心的轨迹方程;
(2)联立直线和抛物线方程,求出交点坐标,假设存在C点,使得△ABC为以CA、CB为两腰的等腰三角形,由三角形的边长相等求不出符合题意的C的坐标,从而说明假设错误,得到结论.
(2)联立直线和抛物线方程,求出交点坐标,假设存在C点,使得△ABC为以CA、CB为两腰的等腰三角形,由三角形的边长相等求不出符合题意的C的坐标,从而说明假设错误,得到结论.
解答:解:(1)∵动圆过定点P(1,0),且与定直线l:x=-1相切,
∴动圆圆心M到定点P(1,0)和到定直线x=-1的距离相等.
∴动圆圆心的轨迹是以P(1,0)为焦点,以x=-1为准线的抛物线,
轨迹方程为y2=4x;
(2)设AB所在直线方程为y=-
(x-1).
由
,消去y得:3x2-10x+3=0.
解得:A(
,
),B(3,-2
),
假设存在这样的C点,使得△ABC为以CA、CB为两腰的等腰三角形,
设C(-1,y),则|AC|=|AB|=|BC|,
∴(
+1)2+(
-y)2=(3-
)2+(2
+
)2①
(3+1)2+(2
+y)2=(3-
)2+(2
+
)2②
解①得:y=
±
.
解②得:y=-2
±
.
∴满足|AC|=|AB|=|BC|的点C不存在.
∴△ABC不能为正三角形.
∴动圆圆心M到定点P(1,0)和到定直线x=-1的距离相等.
∴动圆圆心的轨迹是以P(1,0)为焦点,以x=-1为准线的抛物线,
轨迹方程为y2=4x;
(2)设AB所在直线方程为y=-
| 3 |
由
|
解得:A(
| 1 |
| 3 |
2
| ||
| 3 |
| 3 |
假设存在这样的C点,使得△ABC为以CA、CB为两腰的等腰三角形,
设C(-1,y),则|AC|=|AB|=|BC|,
∴(
| 1 |
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
(3+1)2+(2
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
解①得:y=
2
| ||
| 3 |
4
| ||
| 3 |
解②得:y=-2
| 3 |
4
| ||
| 9 |
∴满足|AC|=|AB|=|BC|的点C不存在.
∴△ABC不能为正三角形.
点评:本题考查了由抛物线的定义求轨迹方程,考查了直线和圆锥曲线的关系,训练了存在性问题的求解方法,是中档题.

练习册系列答案
相关题目
 已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.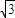 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.