题目内容
用长为18m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,该长方体的最大体积是 .
【答案】分析:根据题意知,长方体的所有棱长和是18m,故可设出宽,用宽表示出长和高,将体积表示成宽的函数,用导数来求其最大值即可.
解答:解:设该长方体的宽是x米,由题意知,其长是2x米,高是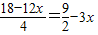 米,(
米,(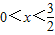 )
)
则该长方体的体积V(x)=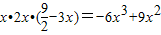 ,
,
由V′(x)=0,得到x=1,且当0<x<1时,V′(x)>0;当1<x< 时,V′(x)<0,
时,V′(x)<0,
即体积函数V(x)在x=1处取得极大值V(1)=3,也是函数V(x)在定义域上的最大值.
所以该长方体体积最大值是3.
故答案为:3.
点评:本小题主要考查长方体的体积及用导数求函数最值等知识,考查化归与转化的数学思想方法,以及推理论证能力和运算求解能力.
解答:解:设该长方体的宽是x米,由题意知,其长是2x米,高是
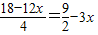 米,(
米,(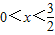 )
)则该长方体的体积V(x)=
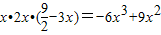 ,
,由V′(x)=0,得到x=1,且当0<x<1时,V′(x)>0;当1<x<
 时,V′(x)<0,
时,V′(x)<0,即体积函数V(x)在x=1处取得极大值V(1)=3,也是函数V(x)在定义域上的最大值.
所以该长方体体积最大值是3.
故答案为:3.
点评:本小题主要考查长方体的体积及用导数求函数最值等知识,考查化归与转化的数学思想方法,以及推理论证能力和运算求解能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目