题目内容

设△ABC不是等腰三角形，，且△ABC的外接圆的圆心为O，两条边上的高的交点为H，若
OH
=m(
OA
+
OB
+
OC
)，则实数m=
 
．
分析：作出如图的图形，可证得四边形AHBE是平行四边形，从研究
OA
+
OB
+
OC
入手，利用三角形法则与图象进行整理，将三者的和用
OH
表示出来．
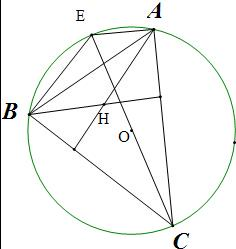解答：精英家教网解：设H是BC边与AC边上高的交点．连CO并延长交圆O于E，连AE，BE．
由CE是圆的直径可知∠CAE=∠CBE=90°，即EA垂直AC，EB垂直BC．
因为H是两边高上的交点，即AH垂直BC，BH垂直AC，
所以有AH平行BE，BH平行AE，
因此四边形BEAH是平行四边形，
从而向量
OA
+
OB
+
OC
=
OA
+
OB
+
EO
=
OA
+
EB
=
OA
+
AH
=
OH
，
即向量
OH
=
OA
+
OB
+
OC
，所以所求值m=1
故答案为1
点评：本题考查三角形的五心，解答本题，关键是根据题意，构造出平行四边形，再利用向量运算，将三个向量的和表示出来，本题中选择入手的位置很关键，此类似于代数中的化简式证明．作题时注意构造法思想的运用，向量在几何中的运用．
练习册系列答案
相关题目
有下列几个命题：①若
a
与
b
-
c
都是非零向量，则“
a
•
b
=
a
•
c
”是“
a
⊥(
b
-
c
)”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是
15
7
；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设
a
，
b
，
c
为同一平面内具有相同起点的任意三个非零向量，且满足
a
与
b
不共线，
a
⊥
c
，|
a
|=|
c
|，则|
b
•
c
|的值一定等于以
a
，
b
为邻边的平行四边形的面积．其中正确命题的序号是
 
．（写出全部正确结论的序号）
已知双曲线的中心在原点O，其中一条准线方程为x=
3
2
，且与椭圆
x2
25
+
y2
13
=1有共同的焦点．
（1）求此双曲线的标准方程；
（2）（普通中学学生做）设直线L：y=kx+3与双曲线交于A、B两点，试问：是否存在实数k，使得以弦AB为直径的圆过点O？若存在，求出k的值，若不存在，请说明理由．
（重点中学学生做）设直线L：y=kx+3与双曲线交于A、B两点，C是直线L1：y=mx+6上任一点（A、B、C三点不共线）试问：是否存在实数k，使得△ABC是以AB为底边的等腰三角形？若存在，求出k的值，若不存在，请说明理由．
已知在关于x的方程ax2-
2
bx+c=0中，a、b、c分别是钝角三角形ABC的三内角A、B、C所对的边，且b是最大边．
（1）求证：该方程有两个不相等的正根；
（2）设方程有两个不相等的正根α、β，若三角形ABC是等腰三角形，求α-β的取值范围．
设A、B、C、D是平面上四个不同的点,其中任意三点不共线.若(+)·()=0,则△ABC是（    ）

A.等腰三角形                               B.直角三角形

C.等腰直角三角形                         D.等边三角形
有下列几个命题：①若
a
与
b
-
c
都是非零向量，则“
a
•
b
=
a
•
c
”是“
a
⊥(
b
-
c
)”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是
15
7
；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设
a
，
b
，
c
为同一平面内具有相同起点的任意三个非零向量，且满足
a
与
b
不共线，
a
⊥
c
，|
a
|=|
c
|，则|
b
•
c
|的值一定等于以
a
，
b
为邻边的平行四边形的面积．其中正确命题的序号是______．（写出全部正确结论的序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网