题目内容
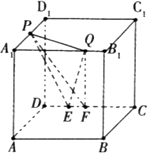
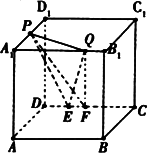
正方体中ABCD-A1B1C1D1,E是C1D1的中点,那么异面直线DE和AC所成角的余弦值等于
.
| ||
| 10 |
| ||
| 10 |
分析:如图连接A1C1,取A1D1的中点F,连接EF,说明异面直线DE和AC所成角,就是异面直线DE和EF所成角,设正方体的棱长为:2,求出DE=DF,EF,即可求出cos∠DEF,得到所以异面直线DE和AC所成角的余弦值.
解答: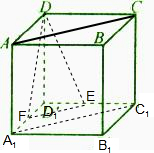 解:如图连接A1C1,取A1D1的中点F,连接EF,易知EF∥A1C1∥AC,
解:如图连接A1C1,取A1D1的中点F,连接EF,易知EF∥A1C1∥AC,
所以异面直线DE和AC所成角,就是异面直线DE和EF所成角,
设正方体的棱长为:2,
所以DE=DF=
=
=
,
EF=
,
所以cos∠DEF=
=
,
所以异面直线DE和AC所成角的余弦值等于
.
故答案为:
.
 解:如图连接A1C1,取A1D1的中点F,连接EF,易知EF∥A1C1∥AC,
解:如图连接A1C1,取A1D1的中点F,连接EF,易知EF∥A1C1∥AC,所以异面直线DE和AC所成角,就是异面直线DE和EF所成角,
设正方体的棱长为:2,
所以DE=DF=
| DD12+D1E2 |
| 22+1 |
| 5 |
EF=
| 2 |
所以cos∠DEF=
| ||||
|
| ||
| 10 |
所以异面直线DE和AC所成角的余弦值等于
| ||
| 10 |
故答案为:
| ||
| 10 |
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.

练习册系列答案
相关题目
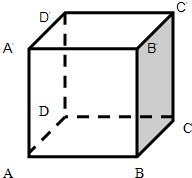 3、如图的正方体ABCD-A′B′C′D′中,异面直线AA′与BC所成的角是( )
3、如图的正方体ABCD-A′B′C′D′中,异面直线AA′与BC所成的角是( ) (2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.
(2004•武汉模拟)(文科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.