Question

（2013•宁波模拟）已知F₁、F₂是椭圆的两个焦点，满足

MF1

⊥

MF2

的点M总在椭圆内部，则椭圆离心率的取值范围是

（O，

2

2

）

．

Answer 1

分析：根据垂直两个向量的数量积为0，可得M点的轨迹是以原点O为圆心，半焦距c为半径的圆．而M总在椭圆内部，说明该圆内含于椭圆，由此建立关于b、c的不等式，结合椭圆的平方关系化简整理即可得到椭圆离心率e的取值范围．

解答：解：设椭圆的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），可得F₁（-c，0），F₂（c，0）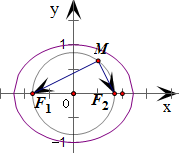
∵

MF1

•

MF2

=0，
∴M点的轨迹是以原点O为圆心，半焦距c为半径的圆．
又∵M点总在椭圆内部，
∴该圆内含于椭圆，可得c＜b，
平方得c²＜b²，即c²＜a²-c²．
∴e²=

c2

a2

＜

1

2

，可得离心率e满足：0＜e＜

2

2

．
故答案为：（O，

2

2

）

点评：本题给满足指向椭圆两个焦点的向量数量积为0，且该点总在椭圆内部，求椭圆的离心率范围，着重考查了椭圆的方程与简单几何性质等知识，属于基础题．