题目内容
3.已知y=(cosx-a)2-1,当cosx=-1时,y取最大值,当cosx=a时,y取最小值,则实数a的范围是[0,1].分析 由条件利用余弦函数的值域,二次函数的性质,求得实数a的范围.
解答 解:对于y=(cosx-a)2-1,由于cosx∈[-1,1],当cosx=-1时,y取最大值,当cosx=a时,y取最小值,
可得0≤a≤1,
故答案为:[0,1].
点评 本题主要考查余弦函数的值域,二次函数的性质应用,属于中档题.

练习册系列答案
相关题目
14.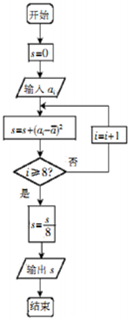 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
 如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )
如图是一个算法的程序框图(其中$\overline{a}$是这8个数据的平均数),若输入ai的值如下表,则输出s的值是( )| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 |
| 39 | 40 | 42 | 42 | 43 | 45 | 46 | 47 |
| A. | A | B. | B | C. | C | D. | D |
11.执行如图所示的程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )
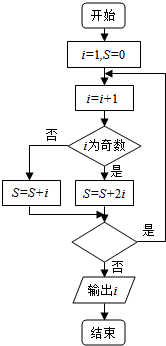

| A. | S≤10? | B. | S≤12? | C. | S≤14? | D. | S≤16? |
8.若某几何体的三视图如图所示,则这个几何体的直观图可以是( )
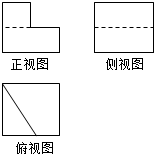

| A. | 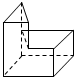 | B. | 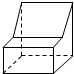 | C. | 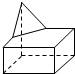 | D. |  |