题目内容
(本小题14分)已知函数 ,设
,设 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。
(Ⅲ)是否存在实数 ,使得函数
,使得函数 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说名理由。
的取值范围,若不存在,说名理由。
【答案】
(1) 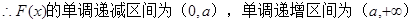
(2) 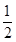
(3)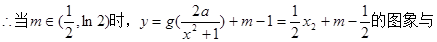
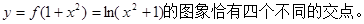
【解析】
试题分析:解.(Ⅰ) 

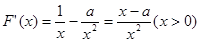
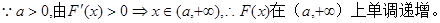
由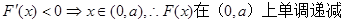 。
。
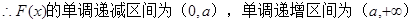 ……3分
……3分
(Ⅱ)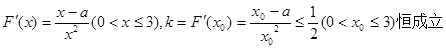
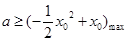 当
当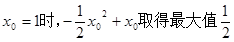
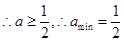 …………………………………………7分
…………………………………………7分
(Ⅲ)若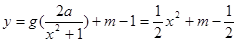 的图象与
的图象与
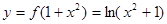 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即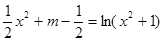 有四个不同的根,亦即
有四个不同的根,亦即
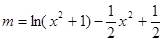 有四个不同的根。
有四个不同的根。
令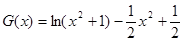 ,……………………10分
,……………………10分
则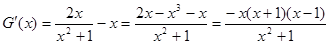
当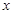 变化时
变化时 的变化情况如下表:
的变化情况如下表:
|
|
|
(-1,0) |
(0,1) |
(1, |
|
|
+ |
- |
+ |
- |
|
|
↗ |
↘ |
↗ |
↘ |
由表格知: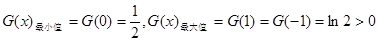 。……12分
。……12分
画出草图和验证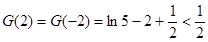 可知,当
可知,当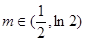 时,
时,
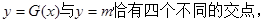

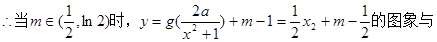
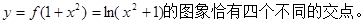 ………………14分
………………14分
考点:本试题考查了函数单调性的知识点。
点评:对于运用导数求解函数的单调区间,一般先求解定义域,再求导数,然后分析导数大于零或小于零的解集得到单调区间,有参数的要加以讨论。而给定函数的单调性递增,确定参数的范围,需要利用导数恒大于等于零,分离参数的思想求解取值范围,这是常考查的常用个的方法,需要熟练的掌握。同时图像的之间的交点问题,一般是利用转换为方程的根的问题来处理得到,属于中档题。

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
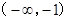
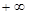 )
)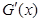 的符号
的符号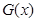 的单调性
的单调性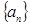 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项. ,
, ,求使
,求使  成立的正整数
成立的正整数 的最小值.
的最小值. 的图像与函数
的图像与函数 的图像关于点
的图像关于点 对称
对称 ,
, 在区间
在区间 上的值不小于6,求实数a的取值范围.
上的值不小于6,求实数a的取值范围. 的图像在[a,b]上连续不断,定义:
的图像在[a,b]上连续不断,定义: ,
, ,其中
,其中 表示函数
表示函数 在D上的最小值,
在D上的最小值, 表示函数
表示函数 对任意的
对任意的 成立,则称函数
成立,则称函数 上的“k阶收缩函数”
上的“k阶收缩函数” ,试写出
,试写出 ,
, 的表达式;
的表达式; 试判断
试判断 ,函数
,函数 是[0,b]上的2阶收缩函数,求b的取值范围
是[0,b]上的2阶收缩函数,求b的取值范围