题目内容
甲、乙、丙三人按下面的规则进行乒乓球比赛:第一局由甲、乙参加而丙轮空,以后每一局由前一局的获胜者与轮空者进行比赛,而前一局的失败者轮空.比赛按这种规则一直进行到其中一人连胜两局或打满6局时停止.设在每局中参赛者胜负的概率均为 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求:(Ⅰ)打满3局比赛还未停止的概率;
(Ⅱ)比赛停止时已打局数ξ的分别列与期望Eξ.
【答案】分析:(1)打满3局比赛还未停止即在三局比赛中没有人连胜两局,分析其可能情况,每局比赛的结果相互独立且互斥,利用独立事件、互斥事件的概率求解即可.
(2)ξ的所有可能值为2,3,4,5,6,分别求出ξ取每一个值的概率,列出分布列即可.
解答:解:令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜.
(Ⅰ)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满3局比
赛还未停止的概率为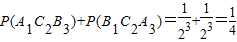 .
.
(Ⅱ)ξ的所有可能值为2,3,4,5,6,且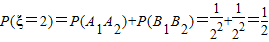 ,
, .
. .
.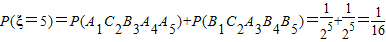 ,
,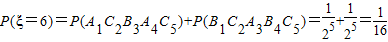 ,
,
故有分布列
从而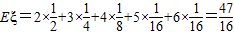 (局).
(局).
点评:本题考查互斥、独立事件的概率,离散型随机变量的分布列和期望等知识,同时考查利用概率知识解决问题的能力.
(2)ξ的所有可能值为2,3,4,5,6,分别求出ξ取每一个值的概率,列出分布列即可.
解答:解:令Ak,Bk,Ck分别表示甲、乙、丙在第k局中获胜.
(Ⅰ)由独立事件同时发生与互斥事件至少有一个发生的概率公式知,打满3局比
赛还未停止的概率为
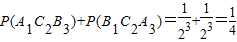 .
.(Ⅱ)ξ的所有可能值为2,3,4,5,6,且
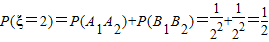 ,
, .
. .
.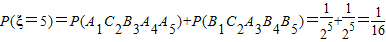 ,
,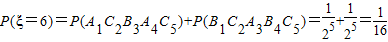 ,
,故有分布列
| ξ | 2 | 3 | 4 | 5 | 6 |
| P |  |  |  | 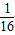 | 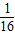 |
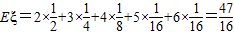 (局).
(局).点评:本题考查互斥、独立事件的概率,离散型随机变量的分布列和期望等知识,同时考查利用概率知识解决问题的能力.

练习册系列答案
相关题目
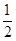 ,且各局胜负相互独立.求:
,且各局胜负相互独立.求: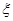 的分布列与期望
的分布列与期望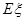 .
.