题目内容
若实数a>0且a≠2,函数f(x)= ax3-
ax3- (a+2)x2+2x+1.
(a+2)x2+2x+1.
(1)证明函数f(x)在x=1处取得极值,并求出函数f(x)的单调区间;
(2)若在区间(0,+∞)上至少存在一点x0,使得f(x0)<1成立,求实数a的取值范围.
解:(1)由已知可得: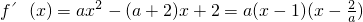 (2分)
(2分)
当a>2时,自变量x,以及f(x),f′(x)的变化情况如下表:
∴函数在x=1处取得极值,f(x)的单调递增区间是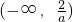 ,(1,+∞)
,(1,+∞)
单调递减区间是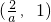 (4分)
(4分)
当0<a<2时自变量x,以及f(x),f′(x)的变化情况如下表:
∴函数f(x)在x=1处取得极值,f(x)的单调递增区间是(-∞,1)和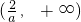 ,单调递减区间是
,单调递减区间是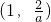 (6分)
(6分)
(2)因为f(0)=1,由(1)知要使在区间(0,+∞)上至少存在一点x0,使得f(x0)<1成立,
只需在区间(0,+∞)上f(x)极小值<1即可 (8分)
当a>2时,f(x)极小值=f(1)=2- <1,所以a>6
<1,所以a>6
当0<a<2时, 恒成立,
恒成立,
所以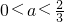
综上所述,实数a的取值范围为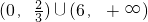 (12分)
(12分)
分析:(1)可以求出函数的导数,利用导数研究单调区间,对于含有一个参数的单调区间问题,要注意讨论参数a的情况,即:0<a<2和a>2来进行讨论,要对x,以及f(x),f′(x)的变化情况表列正确.
(2)本题可以转化为函数f(x)在区间(0,+∞)上f(x)极小值<1即可解答,可以利用(1)的结论,注意对参数a的讨论.
点评:本题考查函数的导数及其应用,求函数的极值,判断函数取得极值的条件以及应用,利用导数研究含一个参数a的函数的单调区间问题,考查了分类讨论思想.
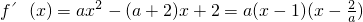 (2分)
(2分)当a>2时,自变量x,以及f(x),f′(x)的变化情况如下表:
| x | 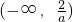 |  | 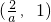 | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
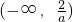 ,(1,+∞)
,(1,+∞)单调递减区间是
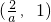 (4分)
(4分)当0<a<2时自变量x,以及f(x),f′(x)的变化情况如下表:
| x | (-∞,1) | 1 | 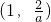 |  | 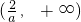 |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |
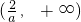 ,单调递减区间是
,单调递减区间是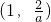 (6分)
(6分)(2)因为f(0)=1,由(1)知要使在区间(0,+∞)上至少存在一点x0,使得f(x0)<1成立,
只需在区间(0,+∞)上f(x)极小值<1即可 (8分)
当a>2时,f(x)极小值=f(1)=2-
 <1,所以a>6
<1,所以a>6当0<a<2时,
 恒成立,
恒成立,所以
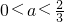
综上所述,实数a的取值范围为
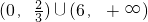 (12分)
(12分)分析:(1)可以求出函数的导数,利用导数研究单调区间,对于含有一个参数的单调区间问题,要注意讨论参数a的情况,即:0<a<2和a>2来进行讨论,要对x,以及f(x),f′(x)的变化情况表列正确.
(2)本题可以转化为函数f(x)在区间(0,+∞)上f(x)极小值<1即可解答,可以利用(1)的结论,注意对参数a的讨论.
点评:本题考查函数的导数及其应用,求函数的极值,判断函数取得极值的条件以及应用,利用导数研究含一个参数a的函数的单调区间问题,考查了分类讨论思想.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 ax3-
ax3- (a+2)x2+2x+1.
(a+2)x2+2x+1.